题目内容
如图所示,光滑水平面上A、B两小球沿同一方向运动,A球的动量为4kgm/s,B球的质量为1kg,速度为6m/s,已知两球相碰后,A球的动量减为原来的一半,方向与原方向一致。求:

(1)碰撞后B球的速度变为多大?
(2)A球的质量范围。

(1)碰撞后B球的速度变为多大?
(2)A球的质量范围。
(1) v B′=8m/s (2)1/4kg≤mA≤3/7 kg
试题分析:(1)根据动量守恒可得: PA+mBvB=PA′+mBv B′
代入数值后可解得:v B′=8m/s
(2)设A球质量为mA,A球能追上B球并与之碰撞,
应满足: vA= PA/ mA> vB
碰撞后A球不能到B球前面,vA′= PA′/ mA< vB′
碰撞过程中能量不能增加
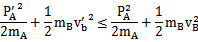
解上述不等式并取交集得1/4kg≤mA≤3/7 kg
点评:本题关键在于小球与滑块碰撞过程,系统受到的外力的合力为零,然后根据系统动量守恒结合能的转化和守恒列式求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
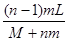
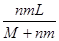
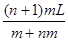
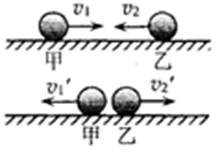


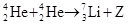 其中( )
其中( )


 )发生α衰变转变成钍核(Th),已知放出的α粒子速度为v0=2.0×106m/s.假设铀核发生衰变时,释放的能量全部转化为α粒子和钍核的动能.试写出铀核衰变的核反应方程并求出钍核(Th)的反冲速度。(结果保留两位有效数字)
)发生α衰变转变成钍核(Th),已知放出的α粒子速度为v0=2.0×106m/s.假设铀核发生衰变时,释放的能量全部转化为α粒子和钍核的动能.试写出铀核衰变的核反应方程并求出钍核(Th)的反冲速度。(结果保留两位有效数字)