题目内容
如图所示,在光滑绝缘的水平直轨道上有两个带电小球a和b,a球质量为2m、带电量为+q,b球质量为m、带电量为+2q,两球相距较远且相向运动。某时刻a、b球的速度大小依次为v和1.5v,由于静电斥力的作用,它们不会相碰。则下列叙述正确的是( )


| A.两球相距最近时,速度大小相等、方向相反 |
| B.a球和b球所受的静电斥力对两球始终做负功 |
| C.a球一直沿原方向运动,b球要反向运动 |
| D.a、b两球都要反向运动,但b球先反向 |
C
试题分析:本题利用动量守恒和功能关系求解比较简单,由于地面光滑,系统所受合外力为零,满足动量守恒条件,当两球速度相当等,系统损失机械能最大,两球相距最近.
水平方向系统动量守恒,由完全非弹性碰撞的知识可知,当两球速度相等时,系统损失机械能最大,两球相距最小,故A错误;
由题意可知,a球动量大于b球动量,因此系统动量水平向右,故b球运动过程中将反向运动而a球将一直沿原方向运动,(或者根据牛顿第二定律分析,此时a、b速度大小一样,而b的减速的加速度大,故b先减为零,然后反向加速运动),因此静电斥力对b球先做负功后做正功,故BD错误,C正确.
故选C.
点评:根据系统运动情况,选用正确规律求解是解题的关键,如在本题中,库仑力为内力,系统外力为零,因此动量守恒,利用动量守恒解答要简单很多.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
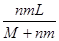
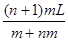
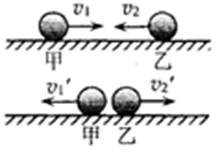
 运动,与质量为m的静止物块发生正撞,碰撞后两者的动量正好相等,两者质量之比M/m可能为
运动,与质量为m的静止物块发生正撞,碰撞后两者的动量正好相等,两者质量之比M/m可能为 He +
He + N
N
 O + ②
O + ②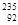 U +
U + n
n Xe +
Xe + Sr +
Sr +