题目内容
8. 如图所示,A、B为两块平行金属板,A板带正电荷、B板带负电荷.两板之间存在着匀强电场,两板间距为d、电势差为U,在B板上开有两个间距为L的小孔.C、D为两块同心半圆形金属板,圆心都在贴近B板的O′处,C带正电、D带负电.两板间的距离很近,两板末端的中心线正对着B板上的小孔,两板间的电场强度可认为大小处处相等,方向都指向O′.半圆形金属板两端与B板的间隙可忽略不计.现从正对B板小孔紧靠A板的O处由静止释放一个质量为m、电荷量为q的带正电的微粒(微粒的重力不计),问:
如图所示,A、B为两块平行金属板,A板带正电荷、B板带负电荷.两板之间存在着匀强电场,两板间距为d、电势差为U,在B板上开有两个间距为L的小孔.C、D为两块同心半圆形金属板,圆心都在贴近B板的O′处,C带正电、D带负电.两板间的距离很近,两板末端的中心线正对着B板上的小孔,两板间的电场强度可认为大小处处相等,方向都指向O′.半圆形金属板两端与B板的间隙可忽略不计.现从正对B板小孔紧靠A板的O处由静止释放一个质量为m、电荷量为q的带正电的微粒(微粒的重力不计),问:(1)微粒穿过B板小孔时的速度多大?
(2)为了使微粒能在C、D板间运动而不碰板,C、D板间的电场强度大小应满足什么条件?
(3)从释放微粒开始,微粒通过半圆形金属板间的最低点P所需时间的表达式.
分析 运用动能定理研究微粒在加速电场的过程.
微粒进入半圆形金属板后,电场力提供向心力,列出等式.
匀加速直线运动和匀速圆周运动运用各自的规律求解时间
解答 解 (1)设微粒穿过B板小孔时的速度为v,根据动能定理,有:
qU=$\frac{1}{2}$mv2,
解得v=$\sqrt{\frac{2qU}{m}}$
(2)微粒进入半圆形金属板后,电场力提供向心力,有:
qE=m$\frac{v2}{R}$,
半径为:R=$\frac{L}{2}$,
联立得:E=$\frac{4U}{L}$.
(3)微粒从释放开始经t1射入B板的小孔,有:d=$\frac{v}{2}$t1,
则有:t1=$\frac{2d}{v}$=2d $\sqrt{\frac{m}{2qU}}$
设微粒在半圆形金属板间运动经过t2第一次到达最低点P点,则有:t2=$\frac{πL}{4v}$=$\frac{πL}{4}$ $\sqrt{\frac{m}{2qU}}$
所以从释放微粒开始,经过t1+t2$(2d+\frac{πL}{4})\sqrt{\frac{m}{2qU}}$微粒第一次到达P点;根据运动的对称性,易知再经过2(t1+t2)微粒再一次经过P点…
所以经过时间为:t=(2k+1)$(2d+\frac{πL}{4})\sqrt{\frac{m}{2qU}}$,(k=0,1,2,…)微粒经过P点.
答:(1)微粒穿过B板小孔时的速度为$\sqrt{\frac{2qU}{m}}$
(2)为了使微粒能在C、D板间运动而不碰板,C、D板间的电场强度大小应满足$\frac{4U}{L}$
(3)从释放微粒开始,微粒通过半圆形金属板间的最低点P所需时间的表达式为(2k+1)$(2d+\frac{πL}{4})\sqrt{\frac{m}{2qU}}$,(k=0,1,2,…).
点评 了解研究对象的运动过程是解决问题的前提,根据题目已知条件和求解的物理量选择物理规律解决问题.圆周运动问题的解决析关键要通过受力分析找出向心力的来源

 阅读快车系列答案
阅读快车系列答案| A. | 0.5 kW | B. | 1.0kW | C. | 2.0kW | D. | 5.0kW |
 如图所示,斜面上有a、b、c、d、e五个点,ab=bc=cd=de.从a点以速度v0水平抛出一个小球,它落在斜而上的b点,若小球从的a点以速度2v0水平抛出,不计空气的阻力,则它将落在斜而上的( )
如图所示,斜面上有a、b、c、d、e五个点,ab=bc=cd=de.从a点以速度v0水平抛出一个小球,它落在斜而上的b点,若小球从的a点以速度2v0水平抛出,不计空气的阻力,则它将落在斜而上的( )| A. | c点 | B. | c与d之间某一点 | C. | d与e之间某一点 | D. | e点 |
| A. | 火星探测器匀速飞行的速度约为$\frac{2πNR}{t}$ | |
| B. | 火星探测器匀速飞行的向心加速度约为$\frac{4{π}^{2}{N}^{2}r}{{t}^{2}}$ | |
| C. | 火星探测器的质量为$\frac{4π{N}^{2}{r}^{3}}{g{R}^{2}{t}^{2}}$ | |
| D. | 火星的平均密度为$\frac{3πM{N}^{2}}{g{R}^{2}t}$ |
 如图所示,在某一点电荷Q产生的电场中,有a、b两点,其中a点的场强大小为Ea,方向与ab连线成30°角;b点的场强大小为Eb,方向与ab连线成60°角.则关于a、b两点场强大小及电势高低,下列说法中正确的是( )
如图所示,在某一点电荷Q产生的电场中,有a、b两点,其中a点的场强大小为Ea,方向与ab连线成30°角;b点的场强大小为Eb,方向与ab连线成60°角.则关于a、b两点场强大小及电势高低,下列说法中正确的是( )| A. | Ea=3Eb,φa<φb | B. | Ea=$\frac{Eb}{3}$,φa>φb | C. | Ea=2Eb,φa>φb | D. | Ea=$\frac{Eb}{2}$,φa<φb |
 如图所示是双缝干涉实验装置的示意图,S为单缝,S1、S2为双缝,P为光屏.用绿光从左边照射单缝S时,可在光屏P上观察到干涉条纹,下列说法正确的是( )
如图所示是双缝干涉实验装置的示意图,S为单缝,S1、S2为双缝,P为光屏.用绿光从左边照射单缝S时,可在光屏P上观察到干涉条纹,下列说法正确的是( )| A. | 减小双缝间的距离,干涉条纹间的距离增大 | |
| B. | 增大双缝到屏的距离,干涉条纹间的距离减小 | |
| C. | 将绿光换为红光,干涉条纹间的距离减小 | |
| D. | 将绿光换为紫光,干涉条纹间的距离增大 |
| A. | 在相同的距离上,电势差大的其场强也必定大 | |
| B. | 场强在数值上等于每单位距离上的电势降落 | |
| C. | 电势降低的方向,必定是电场强度的方向 | |
| D. | 沿着电场线方向,相等距离上的电势降落必定相等 |
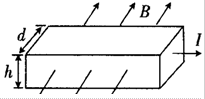 如图所示,宽度为d,厚度为h的导体放在垂直于它的磁感应强度为B的匀强磁场中,当电流通过该导体时,在导体的上、下表面之间会产生电势差,这种现象称为霍尔效应,实验表明:当磁场不太强时,上下表面的电势差U,电流I和B的关系为:U=K$\frac{IB}{d}$,式中的比例系数K称为霍尔系数.设载流子的电量为q,下列说法正确的是( )
如图所示,宽度为d,厚度为h的导体放在垂直于它的磁感应强度为B的匀强磁场中,当电流通过该导体时,在导体的上、下表面之间会产生电势差,这种现象称为霍尔效应,实验表明:当磁场不太强时,上下表面的电势差U,电流I和B的关系为:U=K$\frac{IB}{d}$,式中的比例系数K称为霍尔系数.设载流子的电量为q,下列说法正确的是( )| A. | 载流子所受静电力的大小F=q$\frac{U}{d}$ | |
| B. | 导体上表面的电势一定大于下表面的电势 | |
| C. | 霍尔系数为k=$\frac{1}{nq}$,其中n为导体单位长度上的载流子数 | |
| D. | 载流子所受洛伦兹力的大小f=$\frac{BI}{nhd}$,其中n为导体单位体积内的载流子数 |
