题目内容
13.“利用单摆测重力加速度”的实验如图甲,实验时使摆球在竖直平面内摆动,在摆球运动最低点的左右两侧分别放置一激光光源、光敏电阻(光照时电阻比较小)与某一自动记录仪相连,用刻度尺测量细绳的悬点到球的顶端距离当作摆长,分别测出L1和L2时,该仪器显示的光敏电阻的阻值R随时间t变化的图线分别如图乙、丙所示.
①根据图线可知,当摆长为L1时,单摆的周期T1为2t1,当摆长为L2时,单摆的周期T2为2t2.
②请用测得的物理量(L1、L2、T1 和T2),写出当地的重力加速度g=$\frac{4{π}^{2}({L}_{2}-{L}_{1})}{{T}_{2}^{2}-{T}_{1}^{2}}$.
分析 (1)在一个周期内,摆球两次经过平衡位置,根据该特点结合图象得出单摆的周期;
(2)根据单摆的周期公式T=2π$\sqrt{\frac{L}{g}}$求出L和T2的关系式,根据图象斜率表示的含义求解重力加速度.
解答 解:(1)单摆在一个周期内两次经过平衡位置,每次经过平衡位置,单摆会挡住细激光束,由图乙所示R-t图线可知周期T1=2t1.由图乙所示R-t图线可知周期T2=2t2.
(2)由单摆周期公式T=2π$\sqrt{\frac{L}{g}}$可得:L=$\frac{g}{4{π}^{2}}•{T}^{2}$,
所以在L-T2图象中斜率k=$\frac{g}{4{π}^{2}}$,
根据(1)可知,点(${{T}_{1}}^{2}、{L}_{1}$)和点(${{T}_{2}}^{2}、{L}_{2}$)是L-T2图象中的两点,则有:
k=$\frac{g}{4{π}^{2}}$=$\frac{{L}_{2}-{L}_{1}}{{{T}_{2}}^{2}-{{T}_{1}}^{2}}$
解得:g=$\frac{4{π}^{2}({L}_{2}-{L}_{1})}{{T}_{2}^{2}-{T}_{1}^{2}}$
故答案为:(1)2t1;2t2;(2)$\frac{4{π}^{2}({L}_{2}-{L}_{1})}{{T}_{2}^{2}-{T}_{1}^{2}}$
点评 单摆做简谐运动时,在一个周期内,摆球两次经过平衡位置,熟练应用单摆周期公式即可正确解题,第二问好多同学想不到用图象的方法求解重力加速度,这是一个难点,难度适中.

练习册系列答案
 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
4.列车轨道在转弯处外轨高于内轨,其高度差由转弯半径与火车速度确定.若在某转弯处规定行驶速度为v,则下列说法中正确的是( )
| A. | 当以速度v通过此弯路时,火车重力与轨道面支持力的合力提供向心力 | |
| B. | 当以速度v通过此弯路时,火车受到的摩擦力提供向心力 | |
| C. | 当速度大于v时,轮缘侧向挤压外轨 | |
| D. | 当速度小于v时,轮缘侧向挤压外轨 |
1.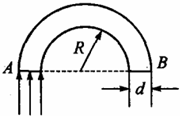 如图所示,一根粗细均匀的半圆形玻璃棒,折射率为1.5,半径为R,两端面A、B均为正方形,宽度为d.令一束平行光垂直于端面A入射,要使入射光线全都从另一端面B射出,则R与d之比的最小值应为( )
如图所示,一根粗细均匀的半圆形玻璃棒,折射率为1.5,半径为R,两端面A、B均为正方形,宽度为d.令一束平行光垂直于端面A入射,要使入射光线全都从另一端面B射出,则R与d之比的最小值应为( )
 如图所示,一根粗细均匀的半圆形玻璃棒,折射率为1.5,半径为R,两端面A、B均为正方形,宽度为d.令一束平行光垂直于端面A入射,要使入射光线全都从另一端面B射出,则R与d之比的最小值应为( )
如图所示,一根粗细均匀的半圆形玻璃棒,折射率为1.5,半径为R,两端面A、B均为正方形,宽度为d.令一束平行光垂直于端面A入射,要使入射光线全都从另一端面B射出,则R与d之比的最小值应为( )| A. | 2 | B. | 1 | C. | 3 | D. | 1.5 |
18.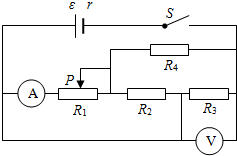 如图所示电路中,电源的内电阻为r、R1、R2、R均为定值电阻,电表均为理想电表.闭合开关S,当滑动变阻器R,的滑动触头P向右滑动时,电流表和电压表的示数变化量的大小分别为△I、△U,下列说法正确的是( )
如图所示电路中,电源的内电阻为r、R1、R2、R均为定值电阻,电表均为理想电表.闭合开关S,当滑动变阻器R,的滑动触头P向右滑动时,电流表和电压表的示数变化量的大小分别为△I、△U,下列说法正确的是( )
 如图所示电路中,电源的内电阻为r、R1、R2、R均为定值电阻,电表均为理想电表.闭合开关S,当滑动变阻器R,的滑动触头P向右滑动时,电流表和电压表的示数变化量的大小分别为△I、△U,下列说法正确的是( )
如图所示电路中,电源的内电阻为r、R1、R2、R均为定值电阻,电表均为理想电表.闭合开关S,当滑动变阻器R,的滑动触头P向右滑动时,电流表和电压表的示数变化量的大小分别为△I、△U,下列说法正确的是( )| A. | 电流表示数变大 | B. | 电压表示数变大 | C. | $\frac{△U}{△I}$<r | D. | $\frac{△U}{△I}$>r |
5.有一质量分布均匀的球状行星,设想把一物体放在该行星的中心位置,则此物体与该行星间的万有引力是( )
| A. | 零 | B. | 无穷大 | C. | 无法确定 | D. | 无穷小 |
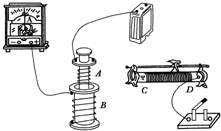 如图所示是为研究电磁感应现象实验所需的各种器材.
如图所示是为研究电磁感应现象实验所需的各种器材. 如图所示,A、B为两块平行金属板,A板带正电荷、B板带负电荷.两板之间存在着匀强电场,两板间距为d、电势差为U,在B板上开有两个间距为L的小孔.C、D为两块同心半圆形金属板,圆心都在贴近B板的O′处,C带正电、D带负电.两板间的距离很近,两板末端的中心线正对着B板上的小孔,两板间的电场强度可认为大小处处相等,方向都指向O′.半圆形金属板两端与B板的间隙可忽略不计.现从正对B板小孔紧靠A板的O处由静止释放一个质量为m、电荷量为q的带正电的微粒(微粒的重力不计),问:
如图所示,A、B为两块平行金属板,A板带正电荷、B板带负电荷.两板之间存在着匀强电场,两板间距为d、电势差为U,在B板上开有两个间距为L的小孔.C、D为两块同心半圆形金属板,圆心都在贴近B板的O′处,C带正电、D带负电.两板间的距离很近,两板末端的中心线正对着B板上的小孔,两板间的电场强度可认为大小处处相等,方向都指向O′.半圆形金属板两端与B板的间隙可忽略不计.现从正对B板小孔紧靠A板的O处由静止释放一个质量为m、电荷量为q的带正电的微粒(微粒的重力不计),问: 如图所示,左侧的圆形导电环半径r=1.0cm,导电环与一个理想变压器的原线圈相连,变压器的副线圈两端与一个电容C=100pF的电容器相连,导电环的电阻不计,环中有垂直于圆环平面的变化磁场,磁感应强度B的变化规律为$\frac{△B}{△t}$=100$\sqrt{2}$•πsinωt,若电容器C所带电荷量的最大值为1.41×10-9C,则所用理想变压器的原、副线圈匝数之比是多少?
如图所示,左侧的圆形导电环半径r=1.0cm,导电环与一个理想变压器的原线圈相连,变压器的副线圈两端与一个电容C=100pF的电容器相连,导电环的电阻不计,环中有垂直于圆环平面的变化磁场,磁感应强度B的变化规律为$\frac{△B}{△t}$=100$\sqrt{2}$•πsinωt,若电容器C所带电荷量的最大值为1.41×10-9C,则所用理想变压器的原、副线圈匝数之比是多少?