题目内容
17. 在均匀介质中位于平衡位置的振源质点O,t=0时沿y轴正方向开始做简谐运动,图为t=1s时的波形,当t=2s时振源第一次回到原点且立即停止振动.则( )
在均匀介质中位于平衡位置的振源质点O,t=0时沿y轴正方向开始做简谐运动,图为t=1s时的波形,当t=2s时振源第一次回到原点且立即停止振动.则( )| A. | 平衡位置xP=-1m处的质点P与平衡位置在xQ=2m处的质点Q在前3s内通过的路程均为4cm | |
| B. | 从t=1s至t=1.5s内质点P的速度不断变小 | |
| C. | 平衡位置xD=4m处的质点D,在t=5s时加速度最大 | |
| D. | 质点P回到平衡位置时,质点D位置坐标为(4m,lcm) |
分析 由题,O为波源且t=0开始向上起振,t=1s末第一次到达波峰,此波形成$\frac{1}{4}$波长的波形,即可知道周期T,读出波长,求出波速.由t=$\frac{x}{v}$求出波传到q和D两质点的时间,即可分析两质点的振动情况.
解答 解:由于当t=2s时振源第一次回到原点,所以振源的周期为:2×2=4s;在t=1s时刻,质点位于最高点,所以该波的振幅是2cm;
A、由图可知,P在1s之前开始运动,在3s前就已经停止了运动,经过 的路程是2倍振幅,即2×2cm=4cm;平衡位置在xQ=2m处的质点Q在第1s末开始运动,在3s末停止运动,经过半个周期,所以经过的路程也是4cm.故A正确;
B、由图可知,该波的传播速度:$v=\frac{△x}{t}=\frac{2}{1}=2$m/s
振源的振动传播到P点的时间:${t}_{1}=\frac{{x}_{P}}{v}=\frac{1}{2}$s,所以在$\frac{1}{4}$周期的时间内,即从t=0.5s至t=1.5s内质点P的速度不断变小.故B正确;
C、波传播到平衡位置xD=4m处的质点D的时间:${t}_{2}=\frac{{x}_{D}}{v}=\frac{4}{2}=2$s,再经过2s,即在第4s末质点D停止运动.故C错误;
D、由B的分析可知,质点P从0.5s末开始振动,则在2.5s末停止运动,此时,质点D以及振动了2.5s-2s=0.5s=$\frac{1}{8}$T,则质点D的位移:
${y}_{D}=A•sin(\frac{2π}{T}•\frac{T}{8})=\frac{\sqrt{2}}{2}A=\sqrt{2}$cm.故D错误.
故选:AB
点评 本题关键确定出波的周期,分析波传播的时间,确定质点振动的状态.而解答本题的难点是能结合振动方程,正确写出质点D在2.5s时刻的位移.

| A. | 地震波是一种复杂的机械波,既有横波又有纵波 | |
| B. | 因为地震波只有纵波,所以破坏性最强 | |
| C. | 地震波传播过程中携带有巨大的能量,传播过程中破坏性很大 | |
| D. | 地震波既有纵波也有横波,且传播速度相等,所以破坏性强 | |
| E. | 地震的震源停止振动时,地震波也立即停止传播,导致受灾范围高度集中 |
| A. | 与原子核外电子发生碰撞 | B. | 与原子核发生 接触碰撞 | ||
| C. | 发生明显衍射 | D. | α粒子与原子核之间的库仑力作用 |
 星际探测是现代航天科技发展的重要课题.如图,某探测器从空间的O点沿直线ON从静止开始以加速度α作匀加速直线运动,两个月后与地球相遇于P点,再经两个月与地球相遇于Q点,已知引力常量G,地球公转周期为T(12个月),忽略天体对探测器的影响,则可估测太阳质量为( )
星际探测是现代航天科技发展的重要课题.如图,某探测器从空间的O点沿直线ON从静止开始以加速度α作匀加速直线运动,两个月后与地球相遇于P点,再经两个月与地球相遇于Q点,已知引力常量G,地球公转周期为T(12个月),忽略天体对探测器的影响,则可估测太阳质量为( )| A. | $\frac{{{π^2}{α^3}{T^4}}}{3546G}$ | B. | $\frac{{{π^2}{α^3}{T^4}}}{3456G}$ | C. | $\frac{3456G}{{{π^2}{α^3}{T^4}}}$ | D. | $\frac{3546G}{{{π^2}{α^3}{T^4}}}$ |
 如图所示,B为理想变压器,接在原线圈上的交流电压U保持不变,R为定值电阻,电压表和电流表均为理想电表.当开关S闭合后,下列说法正确的是( )
如图所示,B为理想变压器,接在原线圈上的交流电压U保持不变,R为定值电阻,电压表和电流表均为理想电表.当开关S闭合后,下列说法正确的是( )| A. | 电流表A1的示数变大 | B. | 电流表A2的示数变小 | ||
| C. | 电压表V的示数变小 | D. | 灯泡L1的亮度变亮 |
 在均匀的介质中,各质点的平衡位置在同一直线上,相邻两个质点的距离均为a,如图甲所示.振动从质点1开始并向右传播,其振动初速度方向竖直向上,经过时间t,前13个质点第一次形成了如图乙所示的波形图,则该波的周期T、波速υ分别是( )(填入选项前的字母,有填错的不得分)
在均匀的介质中,各质点的平衡位置在同一直线上,相邻两个质点的距离均为a,如图甲所示.振动从质点1开始并向右传播,其振动初速度方向竖直向上,经过时间t,前13个质点第一次形成了如图乙所示的波形图,则该波的周期T、波速υ分别是( )(填入选项前的字母,有填错的不得分)| A. | T=$\frac{t}{2}$,υ=$\frac{16a}{t}$ | B. | T=$\frac{2}{3}$t,υ=$\frac{12a}{t}$ | C. | T=t,υ=$\frac{8a}{t}$ | D. | T=$\frac{3}{4}$t,υ=$\frac{6a}{t}$ |
 如图所示,A、B、C、D为四个物体,K1、K2为两个轻弹簧,E为跨过光滑定滑轮的轻绳.物体A在水平地面上,定滑轮左右两段轻绳都处于竖直状态,它们的连接如图所示并都处于静止状态.下列说法正确的是( )
如图所示,A、B、C、D为四个物体,K1、K2为两个轻弹簧,E为跨过光滑定滑轮的轻绳.物体A在水平地面上,定滑轮左右两段轻绳都处于竖直状态,它们的连接如图所示并都处于静止状态.下列说法正确的是( )| A. | K1、K2一定都处于拉伸状态 | |
| B. | K1、K2一定都处于压缩状态 | |
| C. | 有可能K1处于拉伸状态,K2处于压缩状态 | |
| D. | 有可能K1处于压缩状态,K2处于拉伸状态 |
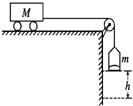 如图,把小车放在光滑的水平桌面上,用轻绳跨过定滑轮使之与盛有沙子的小桶相连,已知小车的质量为M,小桶与沙子的总质量为m,把小车从静止状态释放后,在小桶下落竖直高度为h的过程中,若不计滑轮及空气的阻力,下列说法正确的是( )
如图,把小车放在光滑的水平桌面上,用轻绳跨过定滑轮使之与盛有沙子的小桶相连,已知小车的质量为M,小桶与沙子的总质量为m,把小车从静止状态释放后,在小桶下落竖直高度为h的过程中,若不计滑轮及空气的阻力,下列说法正确的是( )| A. | 绳拉车的力始终为mg | |
| B. | 当M远远大于m时,才可以认为绳拉车的力为mg | |
| C. | 小车获得的动能为$\frac{Mmgh}{M+m}$ | |
| D. | 小车获得的动能为mgh |
 如图所示,竖直放置的光滑圆环,半径为R=0.4m,质量为m=0.4kg小球沿环内侧做完整的圆周运动(如过山车),取g=10m/s2,求:
如图所示,竖直放置的光滑圆环,半径为R=0.4m,质量为m=0.4kg小球沿环内侧做完整的圆周运动(如过山车),取g=10m/s2,求: