题目内容
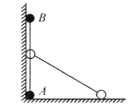
【题目】如图所示，质量相同的小球A、B通过质量不计的细杆相连接，紧靠竖直墙壁放置。由于轻微扰动，小球A、B分别沿水平地面和竖直墙面滑动，滑动过程中小球和杆始终在同一竖直平面内，重力加速度为g，忽略一切摩擦和阻力，下列说法正确的是（ ）
A.B球沿墙下滑的过程中，两球及杆组成的系统机械能守恒但动量不守恒
B.B球从下滑至恰好到达水平面的瞬间，杆对A一直做正功
C.B球从下滑至恰好到达水平面的瞬间,地面对A的支持力先减小后增大
D.当细杆与水平方向成30°角时，小球A的速度大小为v，可求得杆长为
【答案】AD
【解析】
A．B球沿墙下滑的过程中，系统受到的力只有重力做功，所以机械能守恒，但是由于合外力不等于零，所以动量不守恒，故A正确；
BC．初始时刻A球的速度为零，当B球到达水平面时，B的速度向下，此时B球沿着细杆方向的分速度为零，所以此时A球的速度为零，那么在向右端过程中A球必定先加速运动再做减速运动，杆对球A先施加斜向下的推力做正功，此时A对地面压力大于自身重力，后施加斜向上的拉力做负功，此时A对地面压力小于自身重力，故B、C错误；
D．小球A的速度为
时，设小球B的速度大小为
，则有
解得
两球下滑过程中系统的机械能守恒，则有
联立解得
故D正确；
故选AD。
练习册系列答案
相关题目
