题目内容
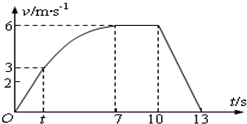
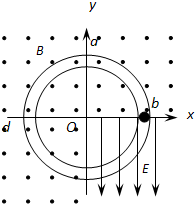
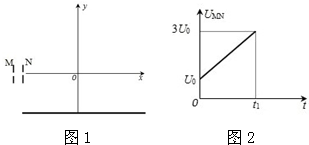
如图1,初速度为零的电子流在平行金属板M、N间被加速,平行金属板M、N间的所加电压按照图2规律变化,且加速电场离y轴距离足够远.电子开始沿x轴运动没有磁场,到达坐标原点才有磁场,电子进入该磁场后均发生270°偏转后沿y轴负方向射出打到x轴下方水平放置的荧光屏上,已知电子的质量为m,电量为e,磁场的磁感强度大小为B,电子在金属板M、N间加速时间极短,可认为粒子在M、N间运动过程电压不变,不计电子之间的相互作用及电子的重力.求:
(1)在t=0时进入电场的电子在磁场中圆周运动的半径大小;
(2)粒子在磁场中运动的时间;
(3)粒子打到荧光屏上的区域范围.
(1)在t=0时进入电场的电子在磁场中圆周运动的半径大小;
(2)粒子在磁场中运动的时间;
(3)粒子打到荧光屏上的区域范围.

(1)t=0时刻进入电场的粒子被加速,由动能定理有eU0=
m
进入磁场后,洛伦兹力提供向心力,则有ev1B=m
联立解得R1=
;
(2)粒子在磁场中圆周运动的周期为:Bev=m
粒子运动的周期为:T=
粒子在磁场中运动的时间为:t=
T
可得:t=
;
(3)设在t=t1时刻进入电场的电子被加速后以速度v2进入磁场,同样发生2700偏转后向下射出打在荧光屏上.在电场中粒子被加速有3eU0=
m
进入磁场后,洛伦兹力提供向心力,则有ev2B=m
联立解得R2=
因而粒子打在荧光屏上的宽度范围为△x=R2-R1
联立解得△x=
(
-1);

答:(1)在t=0时进入电场的电子在磁场中圆周运动的半径R1=
;
(2)粒子在磁场中运动的时间:t=
;
(3)粒子打到荧光屏上的区域范围△x=
(
-1).
| 1 |
| 2 |
| v | 21 |
进入磁场后,洛伦兹力提供向心力,则有ev1B=m
| ||
| R1 |
联立解得R1=
| 1 |
| B |
|
(2)粒子在磁场中圆周运动的周期为:Bev=m
| v2 |
| R |
粒子运动的周期为:T=
| 2πR |
| v |
粒子在磁场中运动的时间为:t=
| 3 |
| 4 |
可得:t=
| 3πm |
| 2Be |
(3)设在t=t1时刻进入电场的电子被加速后以速度v2进入磁场,同样发生2700偏转后向下射出打在荧光屏上.在电场中粒子被加速有3eU0=
| 1 |
| 2 |
| v | 22 |
进入磁场后,洛伦兹力提供向心力,则有ev2B=m
| ||
| R2 |
联立解得R2=
| 1 |
| B |
|
因而粒子打在荧光屏上的宽度范围为△x=R2-R1
联立解得△x=
| 1 |
| B |
|
| 3 |

答:(1)在t=0时进入电场的电子在磁场中圆周运动的半径R1=
| 1 |
| B |
|
(2)粒子在磁场中运动的时间:t=
| 3πm |
| 2Be |
(3)粒子打到荧光屏上的区域范围△x=
| 1 |
| B |
|
| 3 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目