��Ŀ����
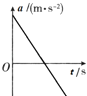
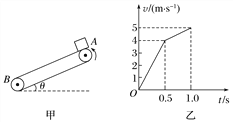
����Ŀ����ͼ����ʾ����б�Ĵ��ʹ��Ժ㶨��������ʱ�����У���t��0ʱ�̣�������Ϊ1.0 kg�����(����Ϊ�ʵ�)���ٶȵط��ڴ��ʹ������϶�A�㣬����1.0 s���������¶˵�B���뿪���ʹ���ȡ�ش��ʹ�����Ϊ�ٶȵ������������ĶԵ��ٶ���ʱ��仯��ͼ����ͼ����ʾ(g��10 m/s2)����
(1)����봫�ʹ���Ķ�Ħ��������
(2)����A��B�Ĺ����У����ʹ���������Ĺ���
���𰸡�(1) ![]() (2) ��3.75 J
(2) ��3.75 J
���������⣺(1)��ͼ���֪�������ǰ0.5 s�ļ��ٶ�Ϊ��![]()
��0.5 s�ļ��ٶ�Ϊ��![]()
�����ǰ0.5 s�ܵ��Ļ���Ħ�����ش��ʹ����£���ţ�ٵڶ����ɵã�
![]()
����ں�0.5 s�ܵ��Ļ���Ħ�����ش��ʹ����ϣ���ţ�ٵڶ����ɵã�
![]()
������ã�![]()
(2)��v��tͼ����������֪����ǰ0.5 s�����Ե�λ��Ϊ��![]()
��Ħ���������������![]()
�ں�0.5 s�����Ե�λ��Ϊ��![]()
��Ħ�������������![]()
���Դ��ʹ�����������ܹ���![]()
������ã�W����3.75 J

��ϰ��ϵ�д�
�����Ŀ