题目内容
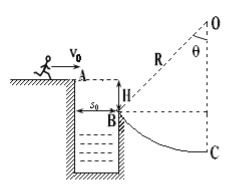
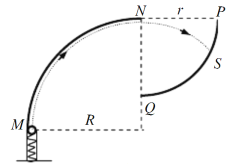
【题目】如图是检验某种防护罩承受冲击能力的装置，MN为半径
、固定于竖直平面内的
光滑圆弧轨道，轨道上端切线水平。PQ为待检验的固定曲面，该曲面为在竖直面内截面半径
的圆弧，圆弧下端切线水平且圆心恰好位于MN轨道的上端点N，M的下端相切处放置竖直向上的弹簧枪，可发射速度不同的质量
的小钢珠，假设某次发射的钢珠沿轨道恰好能经过N点，水平飞出后落到PQ上的S点，取g =10m/s2。求：
（1）小球到达N点时速度
的大小；
（2）发射该钢珠前，弹簧的弹性势能
的大小；
（3）钢珠落到圆弧PQ上S点时速度
的大小。
【答案】（1）
（2）
（3）
【解析】
（1）设钢珠在M轨道最高点的速度为vN，在最高点，由题意mg＝m
①
解得
（2）从发射前到最高点，由机械能守恒定律得：Ep＝mgR+
mv2=0.15J…②
（2）钢珠从最高点飞出后，做平抛运动
x=vt…③
y＝gt2…④
由几何关系：x2+y2=r2…⑤
从飞出M到打在N得圆弧面上，由机械能守恒定律：
mgy+mvs2＝mvN2…⑥
联立①、③、④、⑤、⑥解出所求：vs=4.0m/s
练习册系列答案
相关题目
