题目内容
如图所示，一小球从倾角θ为37º的足够长的斜面顶端作平抛运动，初速度为8m/s，A点是小球离斜面最远点。（1）求小球从抛出到再次落到斜面上的时间？（2）求A点离斜面的距离？（3）将A点前后足够小的一段轨迹视为圆弧，求这段圆弧的半径（曲率半径）及小球在A点的向心加速度（法向加速度）与切向加速度？（第三问仅实验班的同学做，不计入总分）
解决平抛运动的方法是把平抛运动分解到水平方向和竖直方向去研究，水平方向做匀速直线运动，竖直方向做自由落体运动，两个方向上运动的时间相同．
（1）设距离为L，则：水平方向：Lcosθ=V0t 竖直方向：Lsinθ=
gt2
联立解得：t=1.2s
（2）将小球的运动分解为沿斜面和垂直于斜面两个分运动，当垂直斜面方向速度降为零时，小球的速度方向一斜面平行，此时小球与斜面的距离达最大
（3）由题目的介绍可知，求曲率半径也就是求在该点做圆周运动的半径，利用向心力的公式就可以求得．
在A点，把物体的运动看成圆周运动的一部分，物体的重力分力作为向心力，
由向心力的公式得
，所以在其轨迹A处的曲率半径是r=12.5m
向心加速度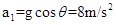
，切向加速度
点评：本题就是对平抛运动规律的直接应用．
（1）设距离为L，则：水平方向：Lcosθ=V0t 竖直方向：Lsinθ=
gt2联立解得：t=1.2s
（2）将小球的运动分解为沿斜面和垂直于斜面两个分运动，当垂直斜面方向速度降为零时，小球的速度方向一斜面平行，此时小球与斜面的距离达最大
（3）由题目的介绍可知，求曲率半径也就是求在该点做圆周运动的半径，利用向心力的公式就可以求得．
在A点，把物体的运动看成圆周运动的一部分，物体的重力分力作为向心力，
由向心力的公式得
，所以在其轨迹A处的曲率半径是r=12.5m向心加速度
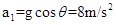，切向加速度点评：本题就是对平抛运动规律的直接应用．
练习册系列答案
中考解读考点精练系列答案
相关题目
将物体水平抛出，它们落地与抛出点的水平距离为s，落地时速度为
，由以上信息可求出物体从抛出到落地所经历的时间。下列有关此时间的表达式错误的是 ( )
的斜面上的M点水平抛出一个小球，小球的初速度为v0，最后小球落在斜面上的N点．则（ ）
