题目内容
如图甲所示,两平行金属板A、B的板长L=0.2m,板间距d=0.2m,两金属板间加如图乙所示的交变电压,并在两板间形成交变的匀强电场,忽略其边缘效应,在金属板上侧有一方向垂直于纸面向里的匀强磁场,其上下宽度D= 0.4m,左右范围足够大,边界MN和PQ均与金属板垂直,匀强磁场的磁感应强度B =1×l0-2T.在极板下侧中点O处有一粒子源,从t=0时起不断地沿着OO’发射比荷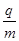 =1×l08 C/kg.初速度为v0=2×l05m/s的带正电粒子,忽略粒子重力、粒子间相互作用以及粒子在极板间飞行时极板间的电压变化.
=1×l08 C/kg.初速度为v0=2×l05m/s的带正电粒子,忽略粒子重力、粒子间相互作用以及粒子在极板间飞行时极板间的电压变化.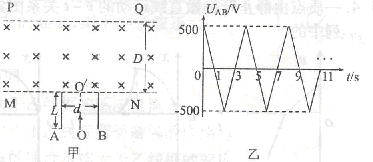
(1)求粒子进入磁场时的最大速率;
(2)对于能从MN边界飞出磁场的粒子,其在磁场的入射点和出射点的间距s是否为定值?若是,求该值;若不是,求s与粒子由O出发的时刻t之间的关系式;
(3)定义在磁场中飞行时间最长的粒子为{A类粒子},求出{A类粒子}在磁场中飞行的时间,以及由O出发的可能时刻.
(1)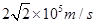 (2)
(2)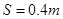 是定值;(3)粒子从O点出发的时刻可能是t=4n+0.4s(n=0,1,2…)
是定值;(3)粒子从O点出发的时刻可能是t=4n+0.4s(n=0,1,2…)
解析试题分析:(1)设偏转的电压为U0时,粒子刚好能经过极板的右边缘射出.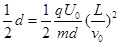 解得:U0=400V.知偏转电压为400V时,粒子恰好能射出电场,且速度最大.
解得:U0=400V.知偏转电压为400V时,粒子恰好能射出电场,且速度最大.
根据动能定理得,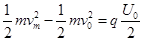
解得: 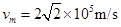
(2)如图,设粒子射出电场速度方向与OO′间夹角为θ.粒子射出电场时速度大小为: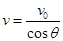
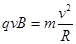 ;由几何关系得:s=2Rcosθ解得:
;由几何关系得:s=2Rcosθ解得: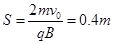 ,是一个定值.
,是一个定值.
(3)如图,{A类粒子}在电场中向B板偏转,在磁场中的轨迹恰好与上边界相切,
则有:R(1+sinθ)="D" 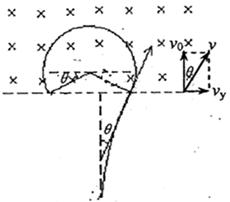
联立以上各式,可得:sinθ=0.6,所以θ=37°;则在磁场中飞行的时间为: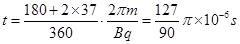
进入磁场时,vy1=v0tanθ=1.5×105m/s
又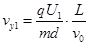 ,对应AB的电压为U1=300V
,对应AB的电压为U1=300V
所以粒子从O点出发的时刻可能是t=4n+0.4s(n=0,1,2…)
考点:带电粒子在匀强电场中的运动;牛顿第二定律;带电粒子在匀强磁场中的运动.

 向右运动。如果加一个竖直向下的匀强磁场,经过一段时间后,该质点的速度第一次变为与初始时刻的速度大小相等、方向相反;如果不加匀强磁场而改为加一个沿水平方向的匀强电场,经过相同的一段时间后,该质点的速度也第一次变为与初始时刻的速度大小相等、方向相反,则所加的匀强磁场的磁感应强度
向右运动。如果加一个竖直向下的匀强磁场,经过一段时间后,该质点的速度第一次变为与初始时刻的速度大小相等、方向相反;如果不加匀强磁场而改为加一个沿水平方向的匀强电场,经过相同的一段时间后,该质点的速度也第一次变为与初始时刻的速度大小相等、方向相反,则所加的匀强磁场的磁感应强度 和所加的匀强电场的电场强度
和所加的匀强电场的电场强度 的比值
的比值 为
为




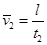 T,粒子的荷质比
T,粒子的荷质比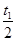 C/kg,不计粒子的重力。问:
C/kg,不计粒子的重力。问: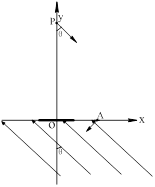

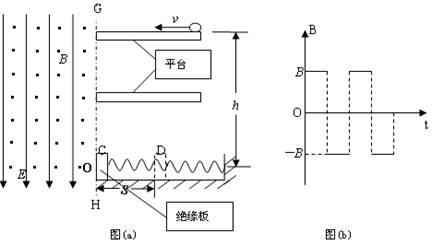
 ,轨道上端接一只阻值为R=0.4
,轨道上端接一只阻值为R=0.4 的电阻器,在导轨间存在垂直于导轨平面的匀强磁场,磁场的磁感应强度B=0.5 T,两轨道之间的距离为L=40cm,且轨道足够长,电阻不计。现将一质量为m="3" g,有效电阻为r=1.0
的电阻器,在导轨间存在垂直于导轨平面的匀强磁场,磁场的磁感应强度B=0.5 T,两轨道之间的距离为L=40cm,且轨道足够长,电阻不计。现将一质量为m="3" g,有效电阻为r=1.0
 ×104V/m。一带正电的粒子(不计重力),其比荷q/m=1.0×104C/kg,从A板静止出发,经过加速电压(电压可调)加速后从坐标原点O沿x轴正方向射入磁场B1。
×104V/m。一带正电的粒子(不计重力),其比荷q/m=1.0×104C/kg,从A板静止出发,经过加速电压(电压可调)加速后从坐标原点O沿x轴正方向射入磁场B1。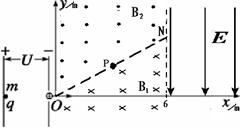

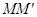 /和
/和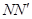 间距为L与水平方向成
间距为L与水平方向成 角,上端接滑动变阻器R,匀强磁场
角,上端接滑动变阻器R,匀强磁场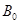 垂直导轨向上,金属棒ab质量为
垂直导轨向上,金属棒ab质量为 垂直横跨在导轨上。滑动变阻器R两端连接水平放置的平行金属板,极板间距为d,板长为2d,匀强磁场B垂直纸面向内。粒子源能发射沿水平方向不同速率的带电粒子,粒子的质量为
垂直横跨在导轨上。滑动变阻器R两端连接水平放置的平行金属板,极板间距为d,板长为2d,匀强磁场B垂直纸面向内。粒子源能发射沿水平方向不同速率的带电粒子,粒子的质量为 ,电荷量为q,ab棒的电阻为r,滑动变阻器的最大阻值为2r,其余部分电阻不计,不计粒子重力。
,电荷量为q,ab棒的电阻为r,滑动变阻器的最大阻值为2r,其余部分电阻不计,不计粒子重力。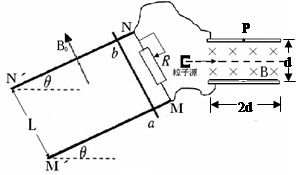
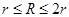 范围调节,总有粒子能匀速穿过平行金属板,求这些粒子的速度范围?
范围调节,总有粒子能匀速穿过平行金属板,求这些粒子的速度范围?