题目内容
如图所示，坐标平面的第I象限内存在大小为E、方向水平向左的匀强电场，足够长的挡板MN垂直x轴放置且距离点O为d．第Ⅱ象 限内存在垂直于纸面向里的匀强磁场．磁感应强 度为B。一质量为m，带电量为－q的粒子（重力忽略不计）若自距原点O为L的A点以一定的 速度垂直x轴进入磁场，则粒子恰好到达O点而不进入电场。现该粒子仍从A点进入磁场但初速 度大小为原来的4倍为使粒子进人电场后能垂直到达挡板MN上，求
（1）粒子第一次从A点进入磁场时，速度的大小：
（2）粒子第二次从A点进入磁场时，速度方向与x轴正向间的夹角大小
（3）粒子打到挡板上时的速度大小。
（1）
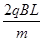；（2）30°或150°（3）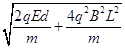
解析试题分析: （1）粒子自距原点O为L的A点以一定的速度垂直x轴进入磁场，恰好到达O点，轨迹为半圆，则得轨迹半径为r=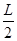
，粒子进入匀强磁场中做匀速圆周运动，由洛伦兹力提供向心力，则有：qv0B=
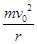，解得v0=；
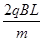（2）设初速度大小为原来的4倍时半径为r1、速度为v1=4v0，由r1=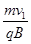
，解得r1=2L
为使粒子进入电场后能垂直到达挡板MN上，粒子必须平行于x轴进入电场，设初速度方向与x轴正向间的夹角大小为θ，（如下图）由几何关系知：sinθ=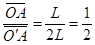
得θ=30°或150°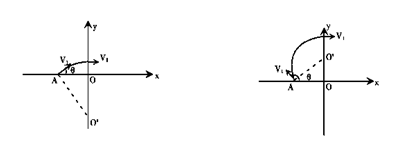 
在电场中电场力对粒子做正功，根据动能定理得：qEd=
-
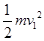
解得：v2=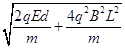
考点：带电粒子在匀强磁场中的运动；牛顿第二定律；向心力；带电粒子在匀强电场中的运动．
练习册系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
，质量不同的带负电的粒子，经过电场加速后进入一速度选择器，从
点进入一等腰直角三角形的有界磁场中，又从斜边射出.速度选择器中垂直纸面向里的匀强磁场的磁感应强度为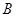
，竖直向下的匀强电场强度为
，有界磁场的磁感应强度为
，直角边长为
，
两点相距为
.求：
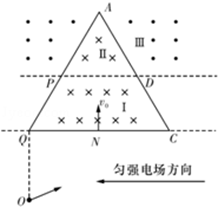
。A点射出的粒子从电场中运动到边界PQ时，两粒子刚好相遇.若粒子质量为m，电荷量为+q，重力不计，求：
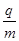=1×l08 C/kg．初速度为v0=2×l05m/s的带正电粒子，忽略粒子重力、粒子间相互作用以及粒子在极板间飞行时极板间的电压变化．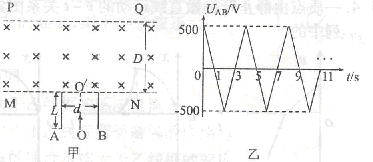
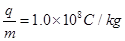，粒子的重力和粒子之间的作用力均可忽略不计。若某时刻粒子源放出的粒子恰能从平行金属板右边缘离开电场（设在每个粒子通过电场区域的时间内，可以把板间的电场看作是恒定的），同时进入金属板右方磁感强度为
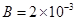T，方向垂直纸面向里的匀强磁场中，一段时间后正粒子垂直打在屏PQ上，屏PQ与金属板右边缘的距离为d=0.5m。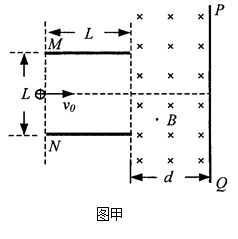
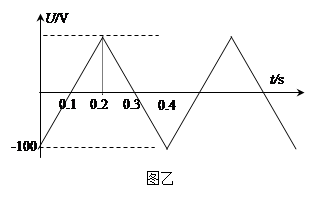
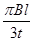，在第Ⅲ、Ⅳ象限中，存在垂直于xOy平面方向的匀强磁场,如图所示,磁感应强度B1＝B，B2＝2B．带电粒子a、b分别从第Ⅰ、Ⅱ象限的P、Q两点（图中没有标出）由静止释放，结果两粒子同时分别进入匀强磁场B1、B2中，再经过时间t第一次经过y轴时恰在点M（0，－
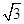l）处发生碰撞，碰撞时两粒子的速度在同一直线上，碰撞前带电粒子b的速度方向与y轴正方向成60°角，不计粒子重力和两粒子间相互作用．求：
