题目内容
(18分)如图(a)所示,有两级光滑的绝缘平台,高一级平台距离绝缘板的中心O的高度为h,低一级平台高度是高一级平台高度的一半.绝缘板放在水平地面上,板与地面间的动摩擦因数为μ,一轻质弹簧一端连接在绝缘板的中心,另一端固定在墙面上。边界GH左边存在着正交的匀强电场和变化的磁场,电场强度为E,磁感应强度变化情况如图(b)所示,磁感应强度大小均为B.有一质量为m、带负电的小球从高一级平台左边缘以一定初速滑过平台后在t=0时刻垂直于边界GH进入复合场中,设小球刚进入复合场时磁场方向向外且为正值.小球做圆周运动至O点处恰好与绝缘板发生弹性碰撞,碰撞后小球立即垂直于边界GH返回并滑上低一级平台,绝缘板从C开始向右压缩弹簧的最大距离为S到达D,求: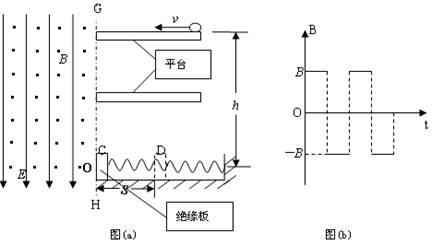
⑴ 磁场变化的周期T;
⑵ 小球从高一级平台左边缘滑出的初速度v;
⑶ 绝缘板的质量M;
⑷ 绝缘板压缩弹簧具有的弹性势能EP.
⑴ 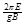 ⑵
⑵ 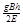 ⑶ 3m ⑷
⑶ 3m ⑷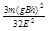 3μmgS.
3μmgS.
解析试题分析:⑴带电小球垂直于边界GH进入复合场,运动到O点恰与绝缘板碰撞,碰后能返回平台,说明小球在复合场中 qE=mg 1分
洛仑兹力做匀速圆周运动的向心力,且经过半个圆周到达O点,碰后再经过半个周期回到二级平台.由 qvB=m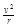 1分
1分
T=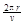 1分
1分
得到带电粒子在磁场运动的周期公式 T=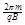 1分
1分
①②消去q,得交变磁场变化的周期 T=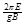 1分
1分
⑵由牛顿第二定律有:qvB=m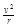
由几何关系有:r=h/2 1分
①③④联立,解得: v=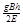 2分
2分
⑶设小球碰撞后的速度大小为V,绝缘板的速度大小为Vm。则题意可知,小球返回的半径r′=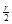 =
=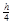 ,又根据r=
,又根据r=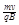 可得:则V=
可得:则V=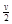 1分
1分
小球与绝缘板碰撞过程中,以小球和绝缘板为系统,动量守恒。
有:mv= mV+MVm 2分
而小球与绝缘板发生的是弹性碰撞,它们构成的系统机械能守恒,有:
有: 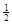 mv2=
mv2=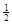 mV2+
mV2+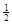 MVm2 2分
MVm2 2分
⑤⑥⑦联立解得:M=3m 1分
⑷绝缘板从C点运动至D点的过程中,根据功能关系有:
EP+μMgS=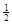 MVm2 2分
MVm2 2分
①③⑤⑥⑦⑨⑩联立解得:EP=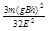 3μmgS. 2分
3μmgS. 2分
考点:本题考查带电粒子在混合场中运动、动能定理、动量守恒、机械能守恒、功能关系。


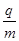 =1×l08 C/kg.初速度为v0=2×l05m/s的带正电粒子,忽略粒子重力、粒子间相互作用以及粒子在极板间飞行时极板间的电压变化.
=1×l08 C/kg.初速度为v0=2×l05m/s的带正电粒子,忽略粒子重力、粒子间相互作用以及粒子在极板间飞行时极板间的电压变化.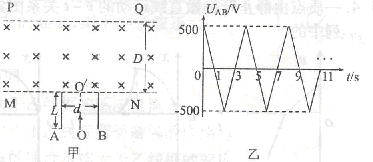
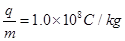 ,粒子的重力和粒子之间的作用力均可忽略不计。若某时刻粒子源放出的粒子恰能从平行金属板右边缘离开电场(设在每个粒子通过电场区域的时间内,可以把板间的电场看作是恒定的),同时进入金属板右方磁感强度为
,粒子的重力和粒子之间的作用力均可忽略不计。若某时刻粒子源放出的粒子恰能从平行金属板右边缘离开电场(设在每个粒子通过电场区域的时间内,可以把板间的电场看作是恒定的),同时进入金属板右方磁感强度为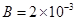 T,方向垂直纸面向里的匀强磁场中,一段时间后正粒子垂直打在屏PQ上,屏PQ与金属板右边缘的距离为d=0.5m。
T,方向垂直纸面向里的匀强磁场中,一段时间后正粒子垂直打在屏PQ上,屏PQ与金属板右边缘的距离为d=0.5m。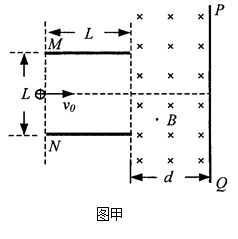
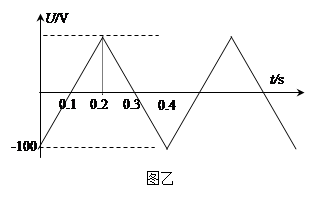

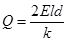 (k为静电力常量)的正点电荷,点电荷产生的电场只存在于CD边界的右侧。今在M点释放一个质量为m、电量为-e的电子(重力不计)。求:
(k为静电力常量)的正点电荷,点电荷产生的电场只存在于CD边界的右侧。今在M点释放一个质量为m、电量为-e的电子(重力不计)。求: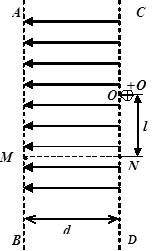
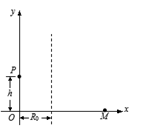
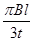 ,在第Ⅲ、Ⅳ象限中,存在垂直于xOy平面方向的匀强磁场,如图所示,磁感应强度B1=B,B2=2B.带电粒子a、b分别从第Ⅰ、Ⅱ象限的P、Q两点(图中没有标出)由静止释放,结果两粒子同时分别进入匀强磁场B1、B2中,再经过时间t第一次经过y轴时恰在点M(0,-
,在第Ⅲ、Ⅳ象限中,存在垂直于xOy平面方向的匀强磁场,如图所示,磁感应强度B1=B,B2=2B.带电粒子a、b分别从第Ⅰ、Ⅱ象限的P、Q两点(图中没有标出)由静止释放,结果两粒子同时分别进入匀强磁场B1、B2中,再经过时间t第一次经过y轴时恰在点M(0,-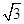 l)处发生碰撞,碰撞时两粒子的速度在同一直线上,碰撞前带电粒子b的速度方向与y轴正方向成60°角,不计粒子重力和两粒子间相互作用.求:
l)处发生碰撞,碰撞时两粒子的速度在同一直线上,碰撞前带电粒子b的速度方向与y轴正方向成60°角,不计粒子重力和两粒子间相互作用.求:
