题目内容
16. 如图所示,倾角为α的斜面上有一个质量为m的物块,在与斜面成β角斜向上的外力F作用下处于静止状态.已知物块和斜面的动摩擦因数μ<tanα,假设物块与斜面间的最大静摩擦力等于滑动摩擦力.求F的大小范围.
如图所示,倾角为α的斜面上有一个质量为m的物块,在与斜面成β角斜向上的外力F作用下处于静止状态.已知物块和斜面的动摩擦因数μ<tanα,假设物块与斜面间的最大静摩擦力等于滑动摩擦力.求F的大小范围.
分析 物体恰好上上滑时,推力最小,受推力、重力、支持力和摩擦力,根据平衡条件列式求解推力的最小值;物体恰好不上滑时,推力最大,受重力、支持力、推力和摩擦力,再次根据平衡条件列式求解推力的最大值;最后联立得到推力的范围
解答 解:分析滑块受力情况,F的最小值Fmin对应静摩擦力沿斜面向上,并取最大值.
此时滑块受力如图所示: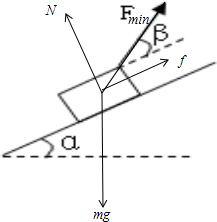
根据平衡有:N+Fminsinβ-mgcosα=0 ①
Fmincosβ+f-mgsinα=0 ②
f=μN ③
由①②两式解得:Fmin=$\frac{mg(sinα-μcosα)}{cosβ-μsinβ}$
F的最大值Fmax对应静摩擦力沿斜面向下,并取最大值,此时受力图如下图所示:
根据平衡有:
N′+Fmaxsinβ-mgcosα=0 ④
Fmaxcosβ-f-mgsinα=0 ⑤
由③④⑤式解得:
Fmax=$\frac{mg(sinα+μcosα)}{cosβ+μsinβ}$
答:F的取值范围为:$\frac{mg(sinα-μcosα)}{cosβ-μsinβ}$≤F≤$\frac{mg(sinα+μcosα)}{cosβ+μsinβ}$.
点评 本题第二问关键抓住恰好不上滑和恰好不下滑的两个临界状态,然后根据共点力平衡条件列式求解.

练习册系列答案
相关题目
6.如图所示是著名的物理实验的装置简图或实验原理图,对这些实验的叙述正确的是( )
| A. |  奥斯特通过如图所示实验发现了电磁感应现象 | |
| B. |  库仑通过如图所示装置测定了万有引力常量 | |
| C. |  安培通过如图所示实验发现了电流的磁效应 | |
| D. |  密立根通过如图所示的实验精确测定了电子的电荷量 |
7.一物体静止在斜面上,下面说法不正确的是( )
| A. | 物体受斜面的作用力,垂直斜面向上 | |
| B. | 物体所受重力可分解为平行于斜面的下滑力和对斜面的正压力 | |
| C. | 只要物体不滑动,它受的摩擦力随斜面倾角的增大而减小 | |
| D. | 一旦物体沿斜面下滑,它所受的摩擦力将随斜面倾角的增大而减小 |
11. 如图所示,倒置的光滑圆锥面内侧,有质量相同的两个小球A、B沿锥面在水平面内做匀速圆周运动.下列关于A、B两球的角速度、线速度和向心加速度的说法中,正确的是( )
如图所示,倒置的光滑圆锥面内侧,有质量相同的两个小球A、B沿锥面在水平面内做匀速圆周运动.下列关于A、B两球的角速度、线速度和向心加速度的说法中,正确的是( )
 如图所示,倒置的光滑圆锥面内侧,有质量相同的两个小球A、B沿锥面在水平面内做匀速圆周运动.下列关于A、B两球的角速度、线速度和向心加速度的说法中,正确的是( )
如图所示,倒置的光滑圆锥面内侧,有质量相同的两个小球A、B沿锥面在水平面内做匀速圆周运动.下列关于A、B两球的角速度、线速度和向心加速度的说法中,正确的是( )| A. | 它们的周期相等 | B. | 它们的向心加速度相等 | ||
| C. | 它们的角速度A比B小 | D. | 它们的线速度A比B小 |
6.如图所示,带箭头的直线是某一电场中的一条电场线,在这条线上有A、B两点,则( )


| A. | 电场线从A指向B,所以EA>EB | |
| B. | 因为A、B在一条电场上,且电场线是直线,所以EA=EB | |
| C. | A点电势比B点电势高 | |
| D. | 不知A、B附近电场线的分布情况,所以不能比较电场强度大小和电势高低 |
 如图所示,光滑水平面AB与竖直面内的半圆形导轨在B点衔接,导轨半径为R,一个质量为m的物块以某一速度向右运动,当它经过B点进入导轨瞬间对导轨的压力为其重力的7倍,而后向上运动恰能完成半圆周运动到C点,求:
如图所示,光滑水平面AB与竖直面内的半圆形导轨在B点衔接,导轨半径为R,一个质量为m的物块以某一速度向右运动,当它经过B点进入导轨瞬间对导轨的压力为其重力的7倍,而后向上运动恰能完成半圆周运动到C点,求: 在图中互成角度的两个力的合成实验中,某同学的实验结果如图所示,其中A为固定橡皮条的图钉,O为橡皮条与细绳结合的位置.如图F是力F1与F2的合力的理论值.(填入F或F′)
在图中互成角度的两个力的合成实验中,某同学的实验结果如图所示,其中A为固定橡皮条的图钉,O为橡皮条与细绳结合的位置.如图F是力F1与F2的合力的理论值.(填入F或F′) 在“伏安法测电阻”实验中,已知待测电阻RX:约5Ω,现有器材如下:
在“伏安法测电阻”实验中,已知待测电阻RX:约5Ω,现有器材如下: