题目内容
5. 如图所示,两平行板间有一匀强电场,板长为L,板间距离为d,在板右端L处有竖直放置的光屏M,一带电荷量为q,质量为m的质点从两板中央射入板间,最后垂直打在M屏上.
如图所示,两平行板间有一匀强电场,板长为L,板间距离为d,在板右端L处有竖直放置的光屏M,一带电荷量为q,质量为m的质点从两板中央射入板间,最后垂直打在M屏上.(1)在图中画出质点运动的大概轨迹图;
(2)求质点从进入半间到运动到M屏上时过程中的时间t;
(3)求质点飞出极板时的速度v;
(4)求板间的电场强度E的大小.
分析 (1)根据题意分析,质点最后垂直打在M屏上,必须考虑质点的重力.质点在平行金属板间轨迹应向上偏转,飞出电场后,质点的轨迹向下偏转,质点才能最后垂直打在M屏上.
(2)第一次偏转质点做类平抛运动,第二次斜向上抛运动,其逆过程是平抛运动.水平方向质点始终做匀速直线运动,质点在板间运动的时间跟它从板的右端运动到光屏的时间相等.
(3)、(4)运用运动的分解法,根据对称性,分析前后过程加速度的关系,再研究电场强度的大小.再由速度公式和速度的合成求质点飞出极板时的速度v.
解答 解:(1)据题分析可知,质点在平行金属板间轨迹应向上偏转,做类平抛运动,飞出电场后,质点的轨迹向下偏转,做斜上抛运动,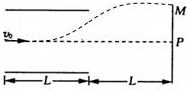 质点才能最后垂直打在M屏上,前后过程质点的运动轨迹有对称性,轨迹如图.
质点才能最后垂直打在M屏上,前后过程质点的运动轨迹有对称性,轨迹如图.
(2)由于质点在水平方向一直做匀速直线运动,所以质点从进入板间到运动到M屏上时过程中的时间 t=$\frac{2L}{{v}_{0}}$.
(3)、(4)根据对称性可知,两次偏转的加速度大小相等,根据牛顿第二定律得
qE-mg=mg,
得到 E=$\frac{2mg}{q}$
质点在电场中的加速度大小为 a=$\frac{qE-mg}{m}$=g
质点飞出极板时的速度 v=$\sqrt{{v}_{0}^{2}+(at)^{2}}$=$\sqrt{{v}_{0}^{2}+(g•\frac{L}{{v}_{0}})^{2}}$=$\sqrt{{v}_{0}^{2}+\frac{{g}^{2}{L}^{2}}{{v}_{0}^{2}}}$
答:(1)在图中画出质点运动的大概轨迹图如图;
(2)质点从进入板间到运动到M屏上时过程中的时间t为$\frac{2L}{{v}_{0}}$;
(3)质点飞出极板时的速度v是$\sqrt{{v}_{0}^{2}+\frac{{g}^{2}{L}^{2}}{{v}_{0}^{2}}}$;
(4)板间的电场强度E的大小是$\frac{2mg}{q}$.
点评 本题是类平抛运动与平抛运动的综合应用,基本方法相同:运动的合成与分解,关键要巧用逆向思维,根据对称性分析.

| A. | 单摆在周期性外力作用下做受迫振动,其振动周期与单摆的摆长无关 | |
| B. | 变化的电场一定产生变化的磁场,变化的磁场一定产生变化的电场 | |
| C. | 在光的双缝干涉实验中,若仅将入射光由红光改为绿光,则干涉条纹间距变窄 | |
| D. | 用透明的标准样板和单色光检查平面的平整度是利用了光的偏振 | |
| E. | 光导纤维丝内芯材料的折射率比外套材料的折射率大 |
| A. | 电磁波只能在真空中传播,机械波不能在真空中传播 | |
| B. | 电磁波都是横波,机械波可能横波也可能是纵波 | |
| C. | 电磁波和机械波都会发生干涉、衍射和多普勒效应 | |
| D. | 不同频率的电磁波在真空中的传播速度都相同 |
| A. | 描述运动物体速度变化快慢的物理量 | |
| B. | 加速度大说明速度变化大 | |
| C. | 加速度没有方向 | |
| D. | 匀速圆周运动的物体加速度为零 |
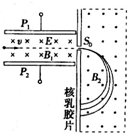 2015年08月21日,美国好奇号火星探测器传回大量火星照片以及相关探测数据,其中不少岩土数据是依托质谱仪进行的分析,该质谱仪模型如下图所示,一束未知粒子进入该质谱仪后的运动轨迹在图中已经标出,则( )
2015年08月21日,美国好奇号火星探测器传回大量火星照片以及相关探测数据,其中不少岩土数据是依托质谱仪进行的分析,该质谱仪模型如下图所示,一束未知粒子进入该质谱仪后的运动轨迹在图中已经标出,则( )| A. | 直线通过复合场区域的粒子具有相同的比荷 | |
| B. | 直线通过复合场区域的粒子具有相同的速度 | |
| C. | 在胶片上打的更远的粒子具有更大的速度 | |
| D. | 在胶片上打的更远的粒子具有更小的比荷 |
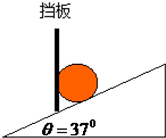 如图,在倾角为37°的光滑斜面上有一块竖直挡板,在挡板和斜面之间有一个重力为20N的光滑小球.
如图,在倾角为37°的光滑斜面上有一块竖直挡板,在挡板和斜面之间有一个重力为20N的光滑小球.
 如图,用绝缘细线和带正电小球做成一单摆.O点是单摆悬点,单摆所在空间有水平向右的匀强电场.现将摆线拉直,将小球从图示位置无初速度释放.已知,摆球质量为m,电量为q,摆线长为1,电场强度E=$\frac{mg}{q}$,θ=$\frac{π}{4}$(摆线与水平位置的夹角)
如图,用绝缘细线和带正电小球做成一单摆.O点是单摆悬点,单摆所在空间有水平向右的匀强电场.现将摆线拉直,将小球从图示位置无初速度释放.已知,摆球质量为m,电量为q,摆线长为1,电场强度E=$\frac{mg}{q}$,θ=$\frac{π}{4}$(摆线与水平位置的夹角)