题目内容
一质量为m的质点,系于长为R的轻绳的一端,绳的另一端固定在空间的O点,假定绳是不可伸长的、柔软且无弹性的.今把质点从O点的正上方离O点的距离为8R/9的O1点以水平的速度v0 = 3/4抛出,如图所示.试求;(1)轻绳即将伸直时,绳与竖直方向的夹角θ为多少?(2)当质点到达O点的正下方时,绳对质点的拉力为多大?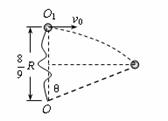
解:(1)第一过程:质点做平抛运动.设绳即将伸直时,绳与竖直方向的夹角为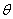 ,如图所示.
,如图所示. 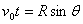
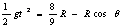 其中
其中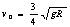 ,解得
,解得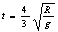
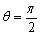
 (2)第二过程:绳绷直过程.绳棚直时,绳刚好水平,如图所示.由于绳不可伸长,故绳绷直时,v0损失,质点仅有速度v⊥,且
(2)第二过程:绳绷直过程.绳棚直时,绳刚好水平,如图所示.由于绳不可伸长,故绳绷直时,v0损失,质点仅有速度v⊥,且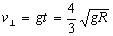 第三过程:小球在竖直平面内做圆周运动.设质点到达O点正下方时,速度为v′,根据机械能守恒守律有:
第三过程:小球在竖直平面内做圆周运动.设质点到达O点正下方时,速度为v′,根据机械能守恒守律有: 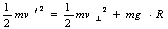
 (2)第二过程:绳绷直过程.绳棚直时,绳刚好水平,如图所示.由于绳不可伸长,故绳绷直时,v0损失,质点仅有速度v⊥,且
(2)第二过程:绳绷直过程.绳棚直时,绳刚好水平,如图所示.由于绳不可伸长,故绳绷直时,v0损失,质点仅有速度v⊥,且
练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
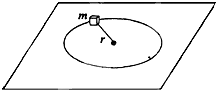 一质量为m的质点,系在细绳的一端,绳的另一端固定在水平面上,水平面粗糙.此质点在该水平面上做半径为r的圆周运动,设质点的最初速率是v0,当它运动一周时,其速率变为
一质量为m的质点,系在细绳的一端,绳的另一端固定在水平面上,水平面粗糙.此质点在该水平面上做半径为r的圆周运动,设质点的最初速率是v0,当它运动一周时,其速率变为 一质量为m的质点,系于长为L的细绳的一端,绳的另一端固定在空间的O点,假定绳是不可伸长、柔软且无弹性的.今把质点从O点的正上方离O点的距离为
一质量为m的质点,系于长为L的细绳的一端,绳的另一端固定在空间的O点,假定绳是不可伸长、柔软且无弹性的.今把质点从O点的正上方离O点的距离为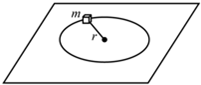 (2011?长春二模)一质量为m的质点,系在轻绳的一端,绳的另一端固定在水平面上,水平面粗糙.此质点在该水平面上做半径为r的圆周运动,设质点的最初速率是v0,当它运动一周时,其速率变为
(2011?长春二模)一质量为m的质点,系在轻绳的一端,绳的另一端固定在水平面上,水平面粗糙.此质点在该水平面上做半径为r的圆周运动,设质点的最初速率是v0,当它运动一周时,其速率变为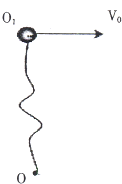 一质量为m的质点,系于长为L的轻绳的一端,绳的另一端固定在空间的O点,假定绳是不可伸长、柔软目无弹性的.今把质点从O点的正上方离O点的距离为
一质量为m的质点,系于长为L的轻绳的一端,绳的另一端固定在空间的O点,假定绳是不可伸长、柔软目无弹性的.今把质点从O点的正上方离O点的距离为