Question

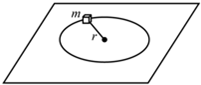（2011?长春二模）一质量为m的质点，系在轻绳的一端，绳的另一端固定在水平面上，水平面粗糙．此质点在该水平面上做半径为r的圆周运动，设质点的最初速率是v₀，当它运动一周时，其速率变为

v0

2

，则（　　）

• A．当它运动一周时摩擦力做的功为-

  3

  8

  m

  v

  2 0

• B．质点与水平面的动摩擦因数为μ=

  3 v 2 0

  16πrg

• C．质点在运动了两个周期时恰好停止
• D．当质点运动一周时的加速度大小为

  v 2 0

  4r

Answer 1

分析：质点在水平面上做圆周运动的过程中，只有摩擦力做功，根据动能定理求出质点运动一周时摩擦力做的功．质点运动一周时摩擦力做的功W=-μmg?2πr，求出μ．根据动能定理求出质点速度减至零时通过的路程．当质点运动一周时质点的加速度是由向心加速度与切向加速度的合成，不等于向心加速度．

解答：解：A、设质点运动一周时摩擦力做的功为W，根据动能定理得：W=

1

2

m(

v0

2

)2-

1

2

m

v

2 0

=-

3

8

m

v

2 0

．故A正确．
    B、W=-

3

8

m

v

2 0

，又W=-μmg?2πr，解得μ=

3 v 2 0

16πrg

．故B正确．
    C、设质点在运动了n周时停止，由动能定理得，-μmg?n?2πr=0-

1

2

m

v

2 0

，n=1.33，所以质点在运动不到两个周期停止运动．故C错误．
    D、当质点运动一周时质点的向心加速度大小为a_n=

( v0 2 )2

r

=

v 2 0

4r

，切向加速度大小为a_t=μg，则加速度a=

a 2 n + a 2 t

＞a_n=

v 2 0

4r

，故D错误．
故选AB

点评：本题是动能定理、向心加速度等知识的综合应用，要注意滑动摩擦力做功与路程有关．