题目内容
一质量为m的质点，系于长为L的细绳的一端，绳的另一端固定在空间的O点，假定绳是不可伸长、柔软且无弹性的．今把质点从O点的正上方离O点的距离为| 8 |
| 9 |
| 3 |
| 4 |
| gL |
分析：细线刚刚绷紧时，将速度沿着细线方向和处置细线方向正交分解，根据平抛运动的规律计算速度的大小，细线刚刚绷紧时，将速度沿着细线方向和处置细线方向正交分解，沿细线方向速度迅速减小为零，垂直细线方向速度不变．
解答：解：小球做平抛运动．设绳即将伸直时，绳与竖直方向的夹角为θ，
则V0t=Rsinθ，
gt2=
L-Lcosθ，
其中V0=
联立解得θ=
，t=
．
即轻绳即将伸直时，绳与竖直方向的夹角为90°．
绳绷直过程．绳棚直时，绳刚好水平，如图所示．
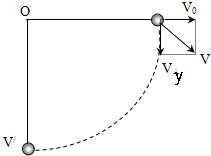
由于绳不可伸长，故绳绷直时，V0损失，小球仅有速度Vy，
所以 Vy=gt=
．
故选D．
则V0t=Rsinθ，
| 1 |
| 2 |
| 8 |
| 9 |
其中V0=
| 3 |
| 4 |
| gL |
联立解得θ=
| π |
| 2 |
| 4 |
| 3 |
|
即轻绳即将伸直时，绳与竖直方向的夹角为90°．
绳绷直过程．绳棚直时，绳刚好水平，如图所示．
由于绳不可伸长，故绳绷直时，V0损失，小球仅有速度Vy，
所以 Vy=gt=
| 4 |
| 3 |
| gL |
故选D．
点评：本题关键是分析清楚小球的运动，平抛运动过程、突然绷紧的瞬时过程；然后根据对各段运用平抛运动位移公式、速度分解法则列式求解．
练习册系列答案
天天向上一本好卷系列答案
相关题目
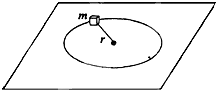一质量为m的质点，系在细绳的一端，绳的另一端固定在水平面上，水平面粗糙．此质点在该水平面上做半径为r的圆周运动，设质点的最初速率是v0，当它运动一周时，其速率变为
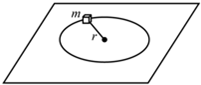（2011?长春二模）一质量为m的质点，系在轻绳的一端，绳的另一端固定在水平面上，水平面粗糙．此质点在该水平面上做半径为r的圆周运动，设质点的最初速率是v0，当它运动一周时，其速率变为
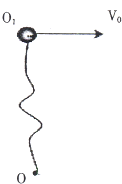一质量为m的质点，系于长为L的轻绳的一端，绳的另一端固定在空间的O点，假定绳是不可伸长、柔软目无弹性的．今把质点从O点的正上方离O点的距离为