题目内容
一质量为m的质点,系在细绳的一端,绳的另一端固定在平面上,此质点在粗糙水平面上作半径为r的圆周运动,设质点的最初速率是V0,当它运动一周时,其速率为
,则摩擦力做的功为
,动摩擦因数等于
.
| v0 |
| 2 |
| -3mv2 |
| 8 |
| -3mv2 |
| 8 |
| 3v02 |
| 16πrg |
| 3v02 |
| 16πrg |
分析:质点在水平面上做圆周运动的过程中,只有摩擦力做功,根据动能定理求出摩擦力做的功.根据滑动摩擦力做功大小等于摩擦力与路程的乘积,求出动摩擦因数.
解答:解:根据动能定理得:摩擦力做的功为W=
m(
)2-
m
=-
m
.又由滑动摩擦力做功大小等于摩擦力与路程的乘积,得W=-μmg?2πr,代入解得,μ=
故答案为:-
m
,
| 1 |
| 2 |
| v0 |
| 2 |
| 1 |
| 2 |
| v | 2 0 |
| 3 |
| 8 |
| v | 2 0 |
| 3v02 |
| 16πrg |
故答案为:-
| 3 |
| 8 |
| v | 2 0 |
| 3v02 |
| 16πrg |
点评:本题中运用动能定理求功是常用思路,难点是抓住滑动摩擦力做功大小与路程有关.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
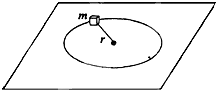 一质量为m的质点,系在细绳的一端,绳的另一端固定在水平面上,水平面粗糙.此质点在该水平面上做半径为r的圆周运动,设质点的最初速率是v0,当它运动一周时,其速率变为
一质量为m的质点,系在细绳的一端,绳的另一端固定在水平面上,水平面粗糙.此质点在该水平面上做半径为r的圆周运动,设质点的最初速率是v0,当它运动一周时,其速率变为 一质量为m的质点,系于长为L的细绳的一端,绳的另一端固定在空间的O点,假定绳是不可伸长、柔软且无弹性的.今把质点从O点的正上方离O点的距离为
一质量为m的质点,系于长为L的细绳的一端,绳的另一端固定在空间的O点,假定绳是不可伸长、柔软且无弹性的.今把质点从O点的正上方离O点的距离为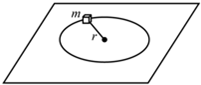 (2011?长春二模)一质量为m的质点,系在轻绳的一端,绳的另一端固定在水平面上,水平面粗糙.此质点在该水平面上做半径为r的圆周运动,设质点的最初速率是v0,当它运动一周时,其速率变为
(2011?长春二模)一质量为m的质点,系在轻绳的一端,绳的另一端固定在水平面上,水平面粗糙.此质点在该水平面上做半径为r的圆周运动,设质点的最初速率是v0,当它运动一周时,其速率变为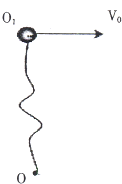 一质量为m的质点,系于长为L的轻绳的一端,绳的另一端固定在空间的O点,假定绳是不可伸长、柔软目无弹性的.今把质点从O点的正上方离O点的距离为
一质量为m的质点,系于长为L的轻绳的一端,绳的另一端固定在空间的O点,假定绳是不可伸长、柔软目无弹性的.今把质点从O点的正上方离O点的距离为