Question

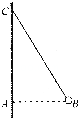
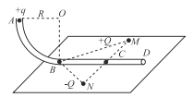
【题目】如图所示，ABCD为竖直放置的光滑绝缘细管道，其中AB部分是半径为R的圆弧形管道，BCD部分是固定的水平管道，两部分管道恰好相切于B。水平面内的M、N、B三点连线构成边长为L的等边三角形，MN连线过C点且垂直于BCD。两个带等量异种电荷的点电荷分别固定在M、N两点，电荷量分别为+Q和-Q。现把质量为m、电荷量为+q的小球（小球直径略小于管道内径，小球可视为点电荷），由管道的A处静止释放。已知静电力常量为k，重力加速度为g。求：

(1)小球运动到B处时受到电场力的大小；

(2)小球运动到圆弧最低点B处时，小球对管道压力的大小。

Answer 1

【答案】（1）；（2）。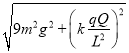

【解析】

（1）设小球在圆弧形管道最低点B处分别受到+Q和-Q的库仑力分别为F1和F2，则：

①

小球沿水平方向受到的电场力为F1和F2的合力F，由平行四边形定则得：

F=2F1cos60° ②

联立①②得：

③；

（2）管道所在的竖直平面是+Q和-Q形成的合电场的一个等势面，小球在管道中运动时，小球受到的电场力和管道对它的弹力都不做功，只有重力对小球做功，小球的机械能守恒，有：

④

解得：

⑤

设在B点管道对小球沿竖直方向的压力为，在竖直方向对小球应用牛顿第二定律得：

⑥

解得：

⑦

设在B点管道对小球在水平方向的压力为，则：

⑧

圆弧形管道最低点B处对小球的压力大小为：

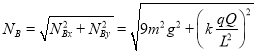⑨

由牛顿第三定律可得小球对圆弧管道最低点B的压力大小为：

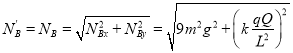⑩