题目内容
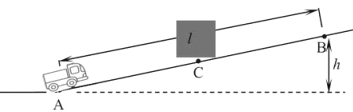
【题目】质量m1=2kg的物体A沿水平面向质量m2=1kg的静止物体B运动,并发生弹性正碰。碰撞前当它们相距L=4m时,物体A的速度v0=5m/s。它们与地面间的动摩擦因数均为μ=0.2,重力加速度g取10m/s2,A、B均可视为质点。求碰撞后A、B都停止运动时它们之间的距离。
【答案】![]()
【解析】试题分析:由动能定理可以求出碰前A的速度。A、B碰撞过程动量守恒,由动量守恒定律可以求出分开后A、B的速度。最后由动能定理可以求出A、B的位移以及它们之间的距离。
设A与B碰撞前的速度为v,对A,由动能定理得: ![]()
代入数据解得: ![]()
A、B碰撞过程动量守恒,以A、B组成的系统为研究对象
以A的初速度方向为正反向,由动量守恒定律得: ![]()
碰撞的过程中没有动能的损失,则: ![]()
代入数据解得: ![]()
A、B相碰后均做匀减速运动,由动能定理得:
对A: ![]()
对B: ![]()
A、B都静止时相距: ![]()
代入数据解得: ![]()

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目