题目内容
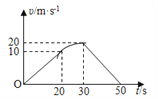
【题目】某日有雾的清晨,一艘质量为m=500t的轮船,从某码头由静止起航做直线运动,并保持发动机的输出功率等于额定功率不变,经t0=10min后,达到最大行驶速度vm=20m/s,雾也恰好散开,此时船长突然发现航线正前方S=480m处,有一只拖网渔船以v=5m/s的速度沿垂直航线方向匀速运动,且此时渔船船头恰好位于轮船的航线上,轮船船长立即下令采取制动措施,附加了恒定的制动力F=1.0×105N,结果渔船的拖网越过轮船的航线时,轮船也恰好从该点通过,从而避免了事故的发生.已知渔船连同拖网总长度L=200m(不考虑拖网渔船的宽度),假定水对船阻力的大小恒定不变,求: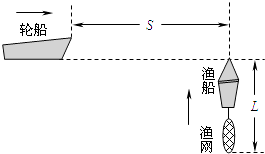
(1)轮船减速时的加速度a;
(2)轮船的额定功率P;
(3)发现渔船时,轮船离开码头的距离.
【答案】
(1)解:渔船通过的时间t= ![]() =40s
=40s
由运动学公式 ![]() ,
,
得到 ![]() =﹣0.4m/s2
=﹣0.4m/s2
答:轮船减速时的加速度a为=﹣0.4m/s2;
(2)轮船做减速运动时,由牛顿第二定律得:﹣( F+Ff)=ma
解得Ff=1.0×105 N
最大速度行驶时,牵引力F=Ff=1.0×105N,
功率P=Fvm=Ff vm=1.0×105×20W=2.0×106 W
答:轮船的额定功率P为2.0×106 W;
(3)由动能定理得 ![]()
解得S1= ![]() m=1.1×104m
m=1.1×104m
答:发现渔船时,轮船离开码头的距离为1.1×104m.
【解析】(1)渔船和轮船运动时间相等,先根据渔船做匀速直线运动,求出运动时间,再根据运动学公式求出轮船运动的加速度。
(2)先根据牛顿第二定律求出摩擦力再根据功率的公式进行求解。
(3)轮船离开码头的过程是以额定功率运动的过程,应用动能定理可以直接求解。
【考点精析】关于本题考查的匀变速直线运动的速度、位移、时间的关系和机车启动,需要了解速度公式:V=V0+at;位移公式:s=v0t+1/2at2;速度位移公式:vt2-v02=2as;以上各式均为矢量式,应用时应规定正方向,然后把矢量化为代数量求解,通常选初速度方向为正方向,凡是跟正方向一致的取“+”值,跟正方向相反的取“-”值;①以恒定功率P启动:机车的运动过程是先作加速度减小的加速运动,后以最大速度v m=P/f 作匀速直线运动;②以恒定牵引力F启动:机车先作匀加速运动,当功率增大到额定功率时速度为v1=P/F,而后开始作加速度减小的加速运动,最后以最大速度vm=P/f作匀速直线运动才能得出正确答案.

 快捷英语周周练系列答案
快捷英语周周练系列答案