题目内容
【题目】如图,质量分别为mA、mB的两个弹性小球A、B静止在地面上方,B球距地面的高度h=0.8m,A球在B球的正上方,先将B球释放,经过一段时间后再将A球释放,当A球下落t=0.3s时,刚好与B球在地面上方的P点相碰,碰撞时间极短,碰后瞬间A球的速度恰为零.已知mB=3mA , 重力加速度大小g=10m/s2 , 忽略空气阻力及碰撞中的动能损失,求: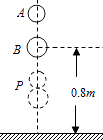
(i)B球第一次到达地面时的速度;
(ii)P点距离地面的高度.
【答案】解:(i)B球释放后做自由落体运动,根据自由落体运动位移速度公式得:
B落地的速度 ![]() …①
…①
(ii)设P点距离地面的高度为h′,碰撞前后,A球的速度分别为v1、v1′,B球的速度分别为v2、v2′,由运动学规律可得:
v1=gt=10×0.3=3m/s…②
由于碰撞时间极短,两球碰撞前后动量守恒,动能守恒,规定向下的方向为正,则:
mAv1﹣mBv2=mBv2′(碰后A球速度为0)…③
![]() mAv12+
mAv12+ ![]() mBv22=
mBv22= ![]() mBv2′2…④
mBv2′2…④
又知mB=3mA…⑤
由运动学及碰撞的规律可得B球与地面碰撞前后的速度大小相等,即碰撞后速度大小为4m/s.
则由运动学规律可得h′= ![]() …⑥
…⑥
联立①~⑥式可得h′=0.75m.
答:(i)B球第一次到达地面时的速度为4m/s;
(ii)P点距离地面的高度为0.75m.
【解析】(1)B球释放后做自由落体运动,根据自由落体运动位移速度公式列式求解即可。
(2)B球与A球碰撞满足动量守恒,B球与地面碰撞前后的速度大小相等,根据运动学规律列式求解即可。

练习册系列答案
相关题目