题目内容
【题目】如图所示，位于竖直面内的xOy直角坐标系的第二象限内存在一匀强电场，电场方向平行于xOy平面，与x轴正方向的夹角θ=60°且斜向上方。整个x轴的负半轴上都分布着粒子发射源，发射源发射的带电粒子完全相同（质量均为m，电荷量均为+q，粒子竖直发射后的初速度大小均为v0，方向均沿y轴正方向），在所有到达y轴正半轴的粒子中自P点发射的粒子经过y轴正半轴时的速度最小。已知带电粒子所受重力大小为其所受电场力大小的
倍，重力加速度为g，不计粒子间的相互作用力。求：
（1）粒子自x轴发射后，在电场中运动时的加速度大小和方向；
（2）自P点发射的粒子经过y轴时的速度大小；
（3）粒子自x轴上的Q点（图中未画出）发射时，粒子经过y轴时的速度方向恰好垂直于y轴，求OQ的距离。（提示：可以参考研究抛体运动时所用的“运动的合成和分解”的思路解题）
【答案】（1）
；与+x轴成
角斜向右下方；（2）
；（3）
【解析】
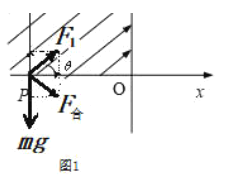
(1)如图1所示，对带电粒子进行受力分析，根据题意可知粒子所受电场力为
现将电场力沿
轴和
轴方向正交分析，可得电场力沿轴方向的分力为
将
与重力
合成得到轴方向的合力为
方向沿轴负方向
然后将
与电场力
沿轴方向的分力
合成的得到最终的合力
方向与
轴成角斜向下
根据牛顿第二定律，粒子的加速度
方向与轴成角斜向右下方。
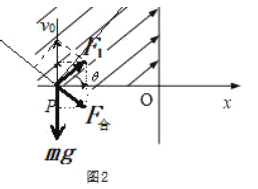
(2)带电粒子在电场中做类斜抛运动，把该运动分解成沿
方向的类竖直上抛运动和垂直于方向的匀速直线运动。如图2所示，将速度
沿方向和垂直于方向正交分解。可知当方向上的速度减为零时粒子的速度最小，最小速度为
（3）如图1所示，将带电粒子的运动看作沿轴方向的类竖直上抛运动和沿轴方向的匀加速度直线运动，在轴方向，其加速度为
在轴方向，其加速度为
当带电粒子垂直打在轴时其沿轴方向的速度为零，这一过程所需时间
其水平距离
为
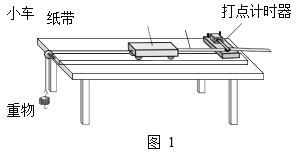
【题目】如图，在 “测定匀变速直线运动加速度”实验中得到的一条纸带上，从O点开始记录几个计数点，依次编为1、2、3、4、5、6，这些相邻的计数点之间还有四个点未画出（打点计时器的电源频率是50Hz），测得s1=1.22cm， s2=2.00cm， s3=2.78cm， s4=3.62cm， s5=4.40cm， s6=5.18cm.．试根据纸带求解以下问题：
（1）接通电源与让释放纸带，这两个操作的先后顺序应当是（ ）
A．先接通电源，后释放纸带 | B．先释放纸带，后接通电源 |
C．释放纸带的同时接通电源 | D．先接通电源或先释放纸带都可以 |
（2）电火花计时器所使用的电源电压是 V
（3）与小车相连的是纸带的 端（选填“左”或“右”）；
（4）两相邻计数点间的时间间隔T= s ；
（5）A点处瞬时速度的大小
m/s；
（6）利用逐差法求小车运动加速度的表达式为： ；（请用S1 、S2、…、 S6和T来表示）
（7）求出的加速度的大小为：
_ ___m/s2．（保留两位有效数字）
