题目内容
13. 一质量为m,带电量为q(q>0)的粒子以速度v垂直进入宽度为L的有界匀强磁场中,如图所示,磁场方向垂直纸面向外,离开磁场的方向与边界成60°角,求匀强磁场的磁感应强度.(不计粒子的重力)
一质量为m,带电量为q(q>0)的粒子以速度v垂直进入宽度为L的有界匀强磁场中,如图所示,磁场方向垂直纸面向外,离开磁场的方向与边界成60°角,求匀强磁场的磁感应强度.(不计粒子的重力)
分析 带电粒子在磁场中做匀速圆周运动,找出圆心、画出轨迹,结合几何关系求轨迹半径,再根据洛伦兹力提供向心力,由牛顿第二定律列式求解.
解答 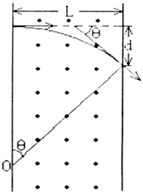 解:如右图为带电粒子的运动轨迹,由几何关系得:θ=60°
解:如右图为带电粒子的运动轨迹,由几何关系得:θ=60°
则粒子的轨迹半径为 r=$\frac{L}{sin60°}$
由牛顿第二定律得 qvB=m$\frac{{v}^{2}}{r}$
联立得 B=$\frac{mvsin60°}{qL}$=$\frac{\sqrt{3}mv}{2qL}$
答:匀强磁场的磁感应强度为$\frac{\sqrt{3}mv}{2qL}$.
点评 本题关键是明确粒子的运动情况和受力情况,找出圆心、画出运动轨迹,然后结合牛顿第二定律列式求解.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
3.质量为m的带电小球在竖直方向的匀强电场中以加速度a=$\frac{1}{3}$g从静止开始竖直向下运动了h的距离,则以下说法正确的是( )
| A. | 在整个过程中小球动能变化了mgh | |
| B. | 下落时电场力的瞬时功率为$\frac{1}{3}$mg$\sqrt{2gh}$ | |
| C. | 在整个过程中电势能增大了$\frac{2}{3}$mgh | |
| D. | 在整个过程中机械能减少了$\frac{1}{3}$mgh |
4.在同一高度,以不同速度同时水平抛出两个钢球,不计空气阻力,则两球( )
| A. | 同时落地 | B. | 水平位移相同 | C. | 加速度不同 | D. | 着地速度相同 |
8.关于机械振动和机械波的说法中正确的是( )
| A. | 有机械波就一定有机械振动,有机械振动不一定有机械波 | |
| B. | 机械波从一种介质传播到另一种介质,频率改变 | |
| C. | 机械波在不同的介质中传播的速度相同 | |
| D. | 机械波在真空中也能传播 |

 一士兵在训练,一根长l=5m的绳上端拴在O点,士兵抓住下端由静止摆下,运动到最低点时松手,而后落到地面上,O点右侧有一堵墙,墙与竖直方向的夹角为37°.为避免士兵撞到墙上,开始时,绳子与竖直方向的夹角θ不应超过多少?(结果用三角函数表示即可).
一士兵在训练,一根长l=5m的绳上端拴在O点,士兵抓住下端由静止摆下,运动到最低点时松手,而后落到地面上,O点右侧有一堵墙,墙与竖直方向的夹角为37°.为避免士兵撞到墙上,开始时,绳子与竖直方向的夹角θ不应超过多少?(结果用三角函数表示即可). 如图所示,一小球从斜面上的A点由静止下滑做匀变速直线运动,先后经过B、C两点,已知小球从B运动到C点的时间为t,B、C两点间的距离为s,小球到达C点时的速度为v,求小球的加速度大小.
如图所示,一小球从斜面上的A点由静止下滑做匀变速直线运动,先后经过B、C两点,已知小球从B运动到C点的时间为t,B、C两点间的距离为s,小球到达C点时的速度为v,求小球的加速度大小.


