题目内容
以V0=2m/s的水平速度，把质量为m=20kg小行李包送到原来静止在光滑水平轨道上的质量为M=30kg的长木板上。如果行李包与长木板之间的动摩擦因数为0．4，取g＝10m/s2，求：
（1）行李包在长木板上滑行多长时间才能与长木板保持相对静止？
（2）长木板至少多长才能使行李包不致滑出木板外？
（1）行李包在长木板上滑行多长时间才能与长木板保持相对静止？
（2）长木板至少多长才能使行李包不致滑出木板外？
（1）
（2）0．3m
（2）0．3m分析：当行李包滑上木板上之后，在摩擦力作用下，行李包作匀减速运动，木板作匀加速运动，最后达到共同速度，设其共同速度为V。对行李包和长木板组成的系统，满足动量守恒条件，根动量守恒定律有：mV0=（M+m）V，得共同速度为
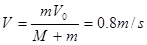
（1）、对行李包，所受动摩擦力为f=µmg，其加速度大小为a=µg=4m/s2
其速度从V0=2m/s减至V=0．8m/s，所用时间为
（2）由运动过程示意图可知，木板滑动距离S1，行李包滑动距离S2及木板长度L间的几何关系为 L= S2－S1 1
对行李包：
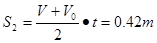2
对长木板：
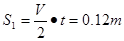3
得木板最小长度L= S2－S1=0．3m
本题主要考查的是动量守恒问题。关键是分析其过程，将动量守恒与运动学公式相结合。
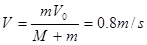
（1）、对行李包，所受动摩擦力为f=µmg，其加速度大小为a=µg=4m/s2
其速度从V0=2m/s减至V=0．8m/s，所用时间为
（2）由运动过程示意图可知，木板滑动距离S1，行李包滑动距离S2及木板长度L间的几何关系为 L= S2－S1 1
对行李包：
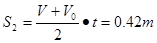2对长木板：
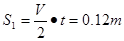3得木板最小长度L= S2－S1=0．3m
本题主要考查的是动量守恒问题。关键是分析其过程，将动量守恒与运动学公式相结合。
练习册系列答案
阅读快车系列答案
相关题目
m的半圆轨道最低点P的切线相平。现有一质量m＝2kg的滑块（可视为质点）以
＝7.5m/s的初速度滑上小车左端，二者共速时滑块刚好在小车的最右边缘，此时小车还未与墙壁碰撞，当小车与墙壁碰撞时即被粘在墙壁上，滑块则离开小车进入圆轨道并顺着圆轨道往上运动，已知滑块与小车表面的滑动摩擦因数μ＝0.5，g取10m/s2．求：
；
=0.4，开始时平板车和滑块共同以v0=2m/s的速度在光滑水平面上向右运动，并与竖直墙壁发生碰撞，设碰撞时间极短且碰撞后平板车速度大小保持不变，但方向与原来相反．平板车足够长，以至滑块不会滑到平板车右端．（取g=10m/s2）求：
