题目内容
如图所示,一质量为m="1" kg、长为L="1" m的直棒上附有倒刺,物体顺着直棒倒刺下滑,其阻力只为物体重力的1/5,逆着倒刺而上时,将立即被倒刺卡住.现该直棒直立在地面上静止,一环状弹性环自直棒的顶端由静止开始滑下,设弹性环与地面碰撞不损失机械能,弹性环的质量M="3" kg,重力加速度g="10" m/s2.求直棒在以后的运动过程中底部离开地面的最大高度. 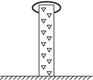

0.45 m
弹性环下落到地面时,速度大小为v1,由动能定理得
Mgl-fl=Mv12/2
解得v1="4" m/s
弹性环反弹后被直棒刺卡住时,与直棒速度相同,
设为v2,由动量守恒定律得Mv1=(M+m)v2
解得v2="3" m/s
直棒能上升的最大高度为 H=v22/2g="0.45" m s
本题考查动能定理的应用和动量守恒定律的理解
Mgl-fl=Mv12/2
解得v1="4" m/s
弹性环反弹后被直棒刺卡住时,与直棒速度相同,
设为v2,由动量守恒定律得Mv1=(M+m)v2
解得v2="3" m/s
直棒能上升的最大高度为 H=v22/2g="0.45" m s
本题考查动能定理的应用和动量守恒定律的理解

练习册系列答案
相关题目
 圆周轨道,圆心O在S的正上方.在O和P两点各有一质量为m的小物块a和b,从同一时刻开始,a自由下落,b沿圆弧下滑.以下说法正确的是( )
圆周轨道,圆心O在S的正上方.在O和P两点各有一质量为m的小物块a和b,从同一时刻开始,a自由下落,b沿圆弧下滑.以下说法正确的是( )




