��Ŀ����
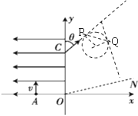
����Ŀ����ͼ��ʾ����ƽ��ֱ������ϵxoy�еĵ�һ �����ڴ��ڴŸ�Ӧǿ�ȴ�СΪB������ֱ������ƽ��������н�Բ����ǿ�ų�����ͼ��δ���������ڵڶ������ڴ�����x�Ḻ�������ǿ�糡��һ����Դ�̶��� x��������Ϊ����L��0����A�㣮����Դ��y���������ͷų��ٶȴ�СΪv�ĵ��ӣ�����ǡ����ͨ��y��������Ϊ��0��2L����C�㣬���Ӿ����ų�ƫת��ǡ�� ��ֱͨ����һ��������x���������15���ǵ�����ON����֪���ӵ�����Ϊm�������Ϊe�����������ӵ�����������֮�������ã�����

��1����ǿ�糡�ĵ糡ǿ��E�Ĵ�С��
��2�������뿪�糡ʱ���ٶȷ�����y��������ļн�����
��3��Բ�δų�����С�뾶Rmin ��
���𰸡���1��![]() ����2������45������3��
����2������45������3��![]() ��
��
����������1����A��C�Ĺ����У���������ƽ���˶����У� ![]()
2L=vt��
������ã� ![]() ����
����
��2������ӵ���C����ٶȴ�СΪvC��������y��������ļн�Ϊ�ȣ��ɶ��ܶ������У� ![]() mvC2-
mvC2-![]() mv2=eEL��
mv2=eEL��
��ã�vC=![]() v
v![]() ��
��
��ã���=45�㣮��
��3�����ӵ��˶��켣ͼ��ͼ�������ڴų���������Բ���˶��İ뾶![]() ��
��
�����ڴų���ƫת120���ֱ��ON�������ų���С�뾶��Rmin=![]() =rsin 60��
=rsin 60��
��������ʽ�ɵã� ![]() ����
����