题目内容

如图所示，一个质量为m，电荷量为e的质子从O点以速度v0垂直NP板射入两板之间区域，两个板间存在垂直纸面向里的匀强磁场，已知两板之间距离为d，板长也为d，O点是NP板的正中间，为使粒子能射出两板间，试求磁感应强度B的大小．
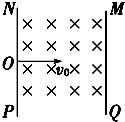
当粒子从a点射出时，轨迹半径最小，设为r1．对应的速度最小，设为v1．当粒子从从b点射出时，轨迹半径最大，设为r2．对应的速度最大，设为v2．根据几何关系得：
r1=
1
4
d，
r22=d2+（r2-
1
2
d）2
则得：r2=
5
4
d，
根据牛顿第二定律得：ev0B=m
v02
r

得：B=
mv0
qr

故有：B1=
4mv0
de
，B2=
5mv0
4de

所以要使粒子能从ab边射出磁场，v0的大小范围为
5mv0
4de
≤B≤
4mv0
de
．
答：要使粒子能从ab边射出磁场，v0的大小范围为
5mv0
4de
≤B≤
4mv0
de
．
练习册系列答案
相关题目
半径为r的光滑圆环固定在竖直平面内，竖直向下的匀强电场强度为E，与圆环所在平面垂直的匀强磁场的磁感强度为B。一质量为m，带正电量为q的球套在光滑圆环上，从A点由静止开始运动，求小球到达最低位置C（∠AOC=900）时：
（1）小球的速率；
（2）小球对圆环压力的大小。
如图所示，在空间存在这样一个磁场区域，以MN为界，上部分的匀强磁场的磁感应强度为B1，下部分的匀强磁场的磁感应强度为B2，B1=2B2=2B0，方向均垂直纸面向内，且磁场区域足够大。在距离界线为h的P点有一带负电荷的离子处于静止状态，某时刻该离子分解成为带电荷的粒子A和不带电的粒子B，粒子A质量为m、带电荷q，以平行于界线MN的速度向右运动，经过界线MN时的速度方向与界线成60°角，进入下部分磁场。当粒子B沿与界线平行的直线到达位置Q点时，恰好又与粒子A相遇。不计粒子的重力。求：
（1）P、Q两点间距离。
（2）粒子B的质量。
一个负离子，质量为m，电量大小为q，以速率V垂直于屏S经过小孔O射入存在着匀强磁场的真空室中(如图11)。磁感应强度B的方向与离子的运动方向垂直，并垂直于图1中纸面向里。

(1)求离子进入磁场后到达屏S上时的位置与O点的距离。
(2)如果离子进入磁场后经过时间t到达位置P，证明:直线O与离子入射方向之间的夹角θ跟t的关系是。
如图所示：在真空中,半径为的圆形区域内存在匀强磁场,磁场方向垂直纸面向里，在磁场右侧有一对平行金属板和，两板间距离为，板长为，板的中心线与磁场的圆心在同一直线上，有一电荷量为、质量为的带电的粒子,以速度从圆周上的点沿垂直于半径并指向圆心的方向进入磁场平面,当从圆周上的点水平飞出磁场时，给、板加上如下图所示电压，最后粒子刚好以平行于板的速度，从板的边缘飞出(不计粒子重力)，求
（1）磁场的磁感应强度；
（2）求交变电压的周期和电压的值；
（3）若时,该粒子从、板右侧沿板的中心线仍以速率向左射入、之间，求粒子从磁场中射出的点到点的距离？
电子质量为m、电量为e，从坐标原点O处沿xOy平面射入第一象限（包括x轴、y轴），射入时速度方向不同，速度大小均为v0，如图所示．现在某一区域加方向向外且垂直于xOy平面的匀强磁场，并保证粒子均从O点进入磁场，磁感应强度为B，若这些电子穿过磁场后都能垂直射到荧光屏MN上，荧光屏与y轴平行，求：
（1）荧光屏上光斑的长度；
（2）所加磁场范围的最小面积．
一质量为m、电荷量为q的带电粒子在磁感应强度为B的匀强磁场中做圆周运动，其效果相当于一环形电流，则此环形电流为多大（　　）
A．
q2B
2πm
B．
2πm
q2B
C．
2πq2
Bm
D．
Bm
2πq2
如图所示，一束质量为m、电荷量为q的带正电粒子从O点由静止开始经过匀强电场加速后，均从边界AN的中点P垂直于AN和磁场方向射入磁感应强度为B=
3
R
2mU
q
的匀强磁场中．已知匀强电场的宽度为d=
1
2
R，匀强磁场由一个长为2R、宽为
1
2
R的矩形区域组成，磁场方向垂直纸面向里，粒子间的相互作用和重力均不计．
（1）若加速电场加速电压为9U，求粒子在电磁场中运动的总时间；
（2）若加速电场加速电压为U，求粒子在电磁场中运动的总时间．
如图所示，带电平行金属板PQ和MN之间的距离为d；两金属板之间有垂直纸面向里的匀强磁场，磁感应强度大小为B．建立如图所示的坐标系，x轴平行于金属板，且与金属板中心线重合，y轴垂直于金属板．区域I的左边界是y轴，右边界与区域II的左边界重合，且与y轴平行；区域II的左、右边界平行．在区域I和区域II内分别存在匀强磁场，磁感应强度大小均为B，区域I内的磁场垂直于Oxy平面向外，区域II内的磁场垂直于Oxy平面向里．一电子沿着x轴正向以速度v0射入平行板之间，在平行板间恰好沿着x轴正向做直线运动，并先后通过区域I和II．已知电子电量为e，质量为m，区域I和区域II沿x轴方向宽度均为
3
mv0
2Be
．不计电子重力．
（1）求两金属板之间电势差U；
（2）求电子从区域II右边界射出时，射出点的纵坐标y；
（3）撤除区域I中的磁场而在其中加上沿x轴正向的匀强电场，使得该电子刚好不能从区域II的右边界飞出．求电子两次经过y轴的时间间隔t．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网