Question

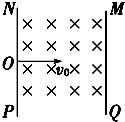
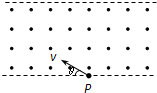
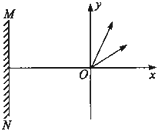
电子质量为m、电量为e，从坐标原点O处沿xOy平面射入第一象限（包括x轴、y轴），射入时速度方向不同，速度大小均为v₀，如图所示．现在某一区域加方向向外且垂直于xOy平面的匀强磁场，并保证粒子均从O点进入磁场，磁感应强度为B，若这些电子穿过磁场后都能垂直射到荧光屏MN上，荧光屏与y轴平行，求：
（1）荧光屏上光斑的长度；
（2）所加磁场范围的最小面积．

Answer 1

（1）要求光斑的长度，只要找到两个边界点即可，电子运动轨迹如图所示：

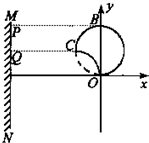
初速度沿x轴正方向的电子，沿弧OB运动到P；初速度沿y轴正方向的电子，沿弧OC运动到Q．
设粒子在磁场中运动的半径为R，由牛顿第二定律得：ev₀B=m

v 20

R

，
解得：R=

mv0

eB

，
由图示可知：PQ=R=

mv0

eB

；
（2）沿任一方向射入第一象限的电子经磁场偏转后都能垂直打到荧光屏MN上，需加最小面积的磁场的边界是以（0，R）为圆心，半径为R的圆的一部分，如图中实线所示．
所以磁场范围的最小面积为：
S=

3

4

πR²+R²-

1

4

πR²=（

π

2

+1）（

mv0

eB

）²．
答：（1）荧光屏上光斑的长度为

mv0

eB

；
（2）所加磁场范围的最小面积为（

π

2

+1）（

mv0

eB

）²．