Question

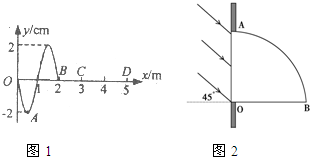
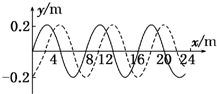
（选修3-4）
（Ⅰ）沿x轴正方向传播的简谐横波在t₁=0s时的波形如图1所示，此时波传播到x=2m处的质点B，质点A恰好位于波谷位置，C、D两个质点的平衡位置分别位于x=3m和x=5m处．当t₂=0.2s时，质点A恰好第一次（从计时后算起） 处于波峰位置，则下列判断中正确的是

 

．
A．该波的波速等于5m/s
B．当t=1.0s时，质点C在平衡位置处且向下运动
C．当t=0.9s时，质点D的位移为-2cm
D．当质点D第一次位于波谷位置时，质点B恰好也位于波谷位置
（Ⅱ）如图2示，AOB是1/4圆柱玻璃砖的截面，玻璃砖的折射率n=

2

，一束平行光以45°入射角射入玻璃砖的OA面，这些光线中只有一部分能从圆柱的AB面上射出，假设凡射到OB面的光线全部被吸收，也不考虑OA面的 反射作用，试问圆柱AB面上能射出光线部分占AB表面的几分之几？

Answer 1

分析：（Ⅰ）根据A质点的运动情况，可求出波的周期，读出波长，求出波速．根据时间与周期的关系，分析质点C的位置及运动状态．结合波形，分析BD状态关系．
（Ⅱ）由sinC=

1

n

求出玻璃砖的临界角．根据折射定律求出光线在AO面上折射角，当光线射到圆弧面上发生全反射时，不能射出，由几何关系得到圆柱AB面上能射出光线部分占AB表面的几分之几．

解答：解：（Ⅰ）A、当t₂=0.2s时，质点A恰好第一次（从计时后算起） 处于波峰位置，则知周期为T=0.4s，由图读出波长为λ=2m，则该波的波速为v=

λ

T

=5m/s．故A正确．
B、t=1.0s=2.5T，波传到C的时间为0.5T，C点的起振方向向上，则在t=1.0s时，质点C在平衡位置处且向上运动．故B错误．
C、t=0.9s=2

1

4

T．波传到C的时间为1.5T，D点的起振方向向上，则t=0.9s时，质点D已振动了

3

4

T，质点D到达波谷，位移为-2cm．故C正确．
D、BD间相距1

1

2

波长，振动情况总是相反，则当质点D第一次位于波谷位置时，质点B恰好位于波峰位置．故D错误．
故选A C
（Ⅱ）由sinC=

1

n

得，临界角 C=45°．
如图所示作出光路图，假设光线从P点入射到C点恰好发生全反射．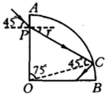
由n=

sin45°

sinr

得，r=30°．∠PCO为临界角，则∠PCO=arcsin

2

2

=45°
则∠POC=180°-45°-60°=75°，∠COB=15°，可以判断出PC以下的光线才能从圆柱面射出，即圆柱面上BC部分有光线射出．

BC

AB

=

15°

90°

=

1

6

，
即圆柱面AB上有

1

6

的表面积能透射出光线来．
答：（Ⅰ）AC；（Ⅱ）圆柱AB面上能射出光线部分占AB表面的

1

6

．

点评：正确地画出光路图是解决第2题的关键，是折射定律和几何知识的结合应用．