��Ŀ����
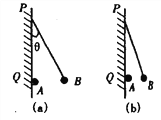
����Ŀ����ͼ��ʾ����һ����ϵ��Ϊk���ᵯ��һ�˹̶����ڱڹ⻬���뾶ΪR�İ����������ײ�O�䴦��OΪ���ģ���������һ��������Ϊm��С��A������С��ֹ��P�㣬OP��ˮƽ�����ļн�Ϊ��=30�㣮����Ϊ������Ϊ2m��С��B������С��ֹ��M�㣨ͼ��δ������������˵����ȷ���ǣ� ��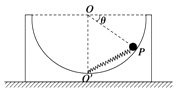
A.������С��B����������СΪ2mg
B.���ɶ�С��A�����������ڶ�С��B��������
C.����ԭ��ΪR+ ![]()
D.OM�ij���Ϊ ![]()
���𰸡�A,C,D
���������⣺C��������Ϊm��С����������֧�����͵��ɵĵ�����ƽ�⣬��ͼ��ʾ��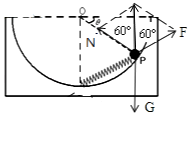
����ƽ���������У�F=N=mg��
�ʵ��ɵ�ԭ��Ϊ��l=R+ ![]() =R+
=R+ ![]() ����C��ȷ��
����C��ȷ��
ABD������Ϊ����Ϊ2m��������뵯�ɼ�ĵ��������OP��ˮƽ����ļн�Ϊ������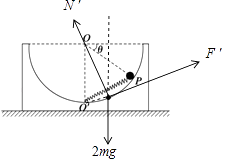
����N����ˮƽ����ļн�Ϊ����F������ֱ����ļн�Ϊ��=45��+ ![]() ��
��
����ƽ��������ˮƽ����N��sin��+F��cos��45��+ ![]() ����
����
��ֱ����N��sin��+F��sin��45��+ ![]() ��=2mg��
��=2mg��
���ݺ��˶��ɣ��У�F��=k[l��2Rsin��45�㩁 ![]() ��]=k[R+
��]=k[R+ ![]() ��2Rsin��45�㩁
��2Rsin��45�㩁 ![]() ��]
��]
������ã�2Rsin��45�㩁 ![]() ��=
��= ![]() ��N��=2mg��
��N��=2mg��
��A��ȷ��B����D��ȷ��
��ѡ��ACD