��Ŀ����
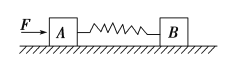
����Ŀ��Ŀ��ͣ���Ǽݿ��е�һ���ؿ���Ŀ������̿ɼ�Ϊ��ͼ��ʾ��ģ�ͣ���һ��ƽֱ��·����A��B��C��D�ĸ�ͣ����־�ˣ�ÿ��������ͣ����־��֮��ľ���Ϊ��x=16m��ij�β���ʱ��ѧԱ��������v0=20m/s���ٶȼ�ʻ����������ʻ��ѧԱ�����ڳ����Ź۲첢��¼ʱ�䣮����ͷ����O��ʱ�����⿼�ٷ���ͣ��ָ�ѧԱ�������ñ��뿪ʼ��ʱ��ѧԱ������t=0.5s�ķ�Ӧʱ���ʼɲ����ɲ����ʼ���ȼ���ֱ���˶���ѧԱ�Ҽ�¼�Լ�ͨ��B��C��ʱ����Ķ����ֱ�Ϊt1=5.5s��t2=7.5s������ֹͣ�˶�ʱ��ͷ����D�˻���5mԶ����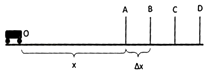
��1��ѧԱ��ͨ��B��C�˵����ʱ����������ƽ���ٶȴ�С��
��2������ɲ��ʱ�ļ��ٶȴ�С
��3��ѧԱ���복ͷ�ľ��룮
���𰸡�
��1��
�⣺ѧԱ��ͨ��B��C�˵����õ�ʱ�䣺
��t=t2��t1=7.5s��5.5s=2s��
��ѧԱ��ͨ��B��C�˵����ʱ����������ƽ���ٶȴ�С��
![]() =
= ![]() =
= ![]() =8m/s��
=8m/s��
��2��
�⣺����ͨ��BC�м�ʱ�̵�˲ʱ�ٶȣ�
v1= ![]() =8m/s��
=8m/s��
ɲ����BC�м�ʱ�̵�ʱ�䣺
t=5.5s+1s��0.5s=6s��
��ɲ��ʱ�ļ��ٶȣ�
a= ![]() =
= ![]() m/s2=��2m/s2��
m/s2=��2m/s2��
������ɲ��ʱ�ļ��ٶȴ�СΪ2m/s2
��3��
�⣺ѧԱ�ҵ���B����ٶ�Ϊ��
vB=v1��a ![]() =8m/s������2m/s2����
=8m/s������2m/s2���� ![]() s=10m/s��
s=10m/s��
��ѧԱ�Ҵ�B�㵽ֹͣ�ľ��룺
x��= ![]() =
= ![]() m=25m��
m=25m��
��������ֹͣ�˶�ʱѧԱ�����־��D�ľ��룺
L��=2��x��x��=2��16m��25m=7m��
��ѧԱ���복ͷ�ľ��룺
��L=L�䩁L=7m��5m=2m
����������1��֪��ѧԱ��ͨ��B��C��ʱ����Ķ����������ó����õ�ʱ�䣬����ƽ���ٶȹ�ʽ���ѧԱ��ͨ��B��C�˵����ʱ����������ƽ���ٶȴ�С����2����������ͨ��BC�м�ʱ�̵�˲ʱ�ٶ������ʱ���ڵ�ƽ���ٶ���ȣ����������ɲ����BC�м�ʱ�����õ�ʱ�䣬Ȼ����ݼ��ٶȹ�ʽ�������ɲ��ʱ�ļ��ٶȴ�С�� ��3�����ݼ��ٶȹ�ʽ���ѧԱ�ҵ���B����ٶȣ�Ȼ�����λ���ٶȹ�ʽ���ѧԱ�Ҵ�B�㵽ֹͣ�ľ��룬����֪��ѧԱ�����־��D�ľ��룬
��ѧԱ�����־��D�ľ����ȥ��ͷ���־��D�ľ��뼴ΪѧԱ���복ͷ�ľ��룮
�����㾫����������Ĺؼ����������ȱ���ֱ���˶����ٶȡ�λ�ơ�ʱ��Ĺ�ϵ�����֪ʶ�������ٶȹ�ʽ��V=V0+at��λ�ƹ�ʽ��s=v0t+1/2at2���ٶ�λ�ƹ�ʽ��vt2-v02=2as�����ϸ�ʽ��Ϊʸ��ʽ��Ӧ��ʱӦ�涨������Ȼ���ʸ����Ϊ��������⣬ͨ��ѡ���ٶȷ���Ϊ�������Ǹ�������һ�µ�ȡ��+��ֵ�����������෴��ȡ��-��ֵ��