Question

【题目】如图甲所示，两水平金属板A、B间的距离为d，极板长为l，A、B右端有一竖直放置的荧光屏，荧光屏距A、B右端的距离为0.7l，A、B两板间加上如图乙所示的周期为T（未知）的方波形电压，电压的正反向值均为U0，A、B间的电场可看作匀强电场，且两板外无电场。现有质量为m、电荷量绝对值为e（重力不计）的电子束，以速度v0沿A、B两板间的中心线OO′射入两板间的偏转电场，所有电子均能通过偏转电场，最后打在荧光屏上。

（1）求电子在电场中的加速度大小及通过偏转电场的时间；

（2）若电子通过偏转电场的时间为方波形电压的一个周期，求从零时刻进入电场的电子在飞出电场时离OO′的距离；

（3）若电子通过偏转电场的时间为方波形电压的半个周期，求电子击中荧光屏上O′点时的速率。（可能会用到652＝4225）

Answer 1

【答案】（1） a=, ；（2）y=；（3）

【解析】

（1）偏转电场的电场强度E=U0/d

根据牛顿第二定律Ee=ma

联立解得：a=

平行极板方向做匀速运动，

通过偏转电场的时间：

（2）电子在偏转电场中沿竖直方向加速半个周期，减速半个周期，最终水平飞出时，电子在竖直方向的位移最大，y=2×=2×()()2=；

（3）当T=2t0时，电子要到达O′点必须在竖直方向有先加速后减速再反向加速过程，并且加速度大小相等，轨迹如图所示：

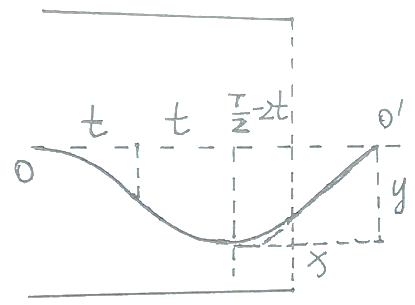
整个过程向下加速的位移和向下减速的位移大小相等，设向下加速时间为t，加速度大小为a，则在竖直方向上有：

③

④

⑤

联立②③④⑤得t=t0/3=T/6，

所以到达O′点的电子经过偏转电场时电子做功，

W=eE×= ，

电子从K到O过程由动能定理得：。