题目内容
【题目】如图所示为一横截面是直角三角形ABC的透明介质，其中∠B=90°，∠C=30°， D、E点是斜边的三等分点，AC=3l，在底边BA的延长线上有一复色点光源S，光源S与A的距离为l。光源S发出两束色光a、b分别照射到斜边上的E、D点，经过斜边折射后进入透明介质中的光线均平行于底边AB，然后在BC边第一次射出透明介质。已知光在真空中的速度为c。求：
①透明介质对a光的折射率；
②b光第一次在透明介质中传播的时间。
【答案】（1）
（2）
【解析】①由几何关系易得： 
,
①
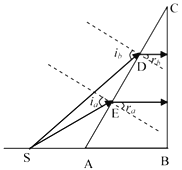
由折射率的定义式得
②
②设
，则
③
由正弦定理有： 
④
解得 
⑤
由三角函数知识得： 
⑥
由几何关系得 
⑦
由折射率的定义式知
⑧
b光在透明介质中的速度
⑨
b光第一次在透明介质中传播的距离为： 
⑩
b光第一次在透明介质中传播的时间为
叠加：解答本题的关键是正确画出光路图，依据几何关系确定折射角以及光在三棱镜中传播的距离，再结合折射定律、光速公式解题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
