题目内容

（18分）如图所示，水平传送带上A、B两端点间 距L= 4m，半径R=1m的光滑半圆形轨道固定于竖直平面内，下端与传送带B相切。传送带以v0 = 4m/s的速度沿图示方向匀速运动，质量m =1kg的小滑块由静止放到传送带的A端，经一段时间运动到B端，滑块与传送带间的动摩擦因数μ = 0.5，取g=10m/s2。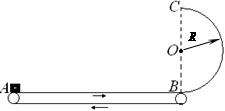

（1）求滑块到达B端的速度；
（2）求滑块由A运动到B的过程中，滑块与传送带间摩擦产生的热量；
（3）仅改变传送带的速度，其他条件不变，计算说明滑块能否通过圆轨道最高点C。

（1）4m/s  （2）8J   （3）不能通过圆轨道最高点

解析试题分析：⑴滑块在传送带上先向右做加速运动，设当速度v = v0时已运动的距离为x
根据动能定理 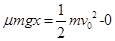    （3分）
得x=1.6m＜L， 所以滑块到达B端时的速度为4m/s           （2分）
⑵设滑块与传送带发生相对运动的时间为t，则 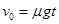          （1分）
滑块与传送带之间产生的热量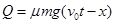          （2分）
解得  Q = 8J          （2分）
⑶设滑块通过最高点C的最小速度为
经过C点：根据向心力公式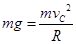          （2分）
从B到C过程：根据动能定理 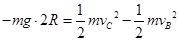            （3分）
解得 经过B的速度m/s
从A到B过程：若滑块一直加速，根据动能定理 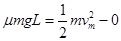    （2分）
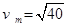解得 m/s
由于速度vm＜vB，所以仅改变传送带的速度，滑块不能通过圆轨道最高点 （1分）
考点：本题考查了动能定理和圆周运动。

练习册系列答案
相关题目

如图，半径R=0.4m的圆盘水平放置，绕竖直轴OO′匀速转动，在圆心O正上方h=0.8m高处固定一水平轨道PQ，转轴和水平轨道交于O′点。一质量m=1kg的小车（可视为质点），在F=4N的水平恒力作用下，从O′左侧x0=2m处由静止开始沿轨道向右运动，力作用一段距离后撤去，当小车运动到O′点时，从小车上自由释放一小球，此时圆盘半径OA与x轴重合。规定经过O点水平向右为x轴正方向。小车与轨道间的动摩擦因数μ=0.2，g取10m/s2。

（1）若小球刚好落到A点，求小车运动到O′点的速度；
（2）为使小球刚好落在A点，圆盘转动的角速度应为多大？
（3）为使小球能落到圆盘上，求水平拉力F作用的距离范围。

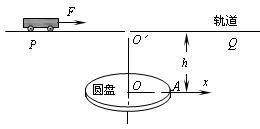
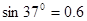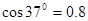(19分) 如图所示，在一倾角为370的绝缘斜面下端O，固定有垂直于斜面的绝缘挡板。斜面ON段粗糙，长度s=0.02m，NM段光滑，长度L=0.5m。在斜面的所在区域有竖直向下的匀强电场，场强为2×lo5 N/C。有一小滑块质量为2×10－3 kg，带正电，电量为 1×l0－7C，小滑块与ON段表面的动摩擦因数为0.75。将小滑块从M点由静止释放，在运动过程中没有电量损失，与挡板相碰后原速返回。已知，，g取 l0m/s2．求：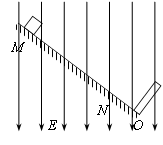

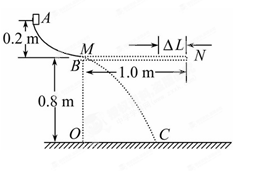
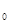(1)小滑块第一次过N点的速度大小；
(2)小滑块最后停在距离挡板多远的位置；
(3)小滑块在斜面上运动的总路程。

如图所示，在竖直平面内有半径为R="0.2" m的光滑1/4圆弧AB，圆弧B处的切线水平，O点在B点的正下方，B点高度为h="0.8" m。在B端接一长为L="1.0" m的木板MN。一质量为m="1.0" kg的滑块，与木板间的动摩擦因数为0.2，滑块以某一速度从N点滑到板上，恰好运动到A点。 (g取10 m/s2)求：

(1)滑块从N点滑到板上时初速度的速度大小；
(2)从A点滑回到圆弧的B点时对圆弧的压力；
(3)若将木板右端截去长为ΔL的一段，滑块从A端静止释放后，将滑离木板落在水平面上P点处，要使落地点P距O点最远，ΔL应为多少？

如图所示，在绝缘水平面上，相距为L的A、B两点处分别固定着两个带电量相等的正电荷，a、b是AB连线上的两点，其中Aa＝Bb＝L／4，O为AB连线的中点，一质量为m带电量为+q的小滑块（可以看作质点）以初动能E从a点出发，沿直线AB向b点运动，其中小滑块第一次经过O点时的动能为初动能的n倍（n>l），到达b点时动能恰好为零,小滑块最终停在O点，求：

（1）小滑块与水平面间的动摩擦因数；
（2）O、b两点间的电势差；
（3）小滑块运动的总路程。

如图所示，在绝缘水平面上相距为L的A、B两点分别固定着等量正点电荷.O为AB连线的中点，C、D是AB连线上两点，其中AC=CO=OD=DB=1/4L.一质量为m电量为+q的小滑块（可视为质点）以初动能E从C点出发，沿直线AB向D运动，滑块第一次经过O点时的动能为kE（k＞1），到达D点时动能恰好为零，小滑块最终停在O点，求：

（1）小滑块与水平面之间的动摩擦因数μ.
（2）OD两点间的电势差UOD.
（3）小滑块运动的总路程s.

如图所示，光滑绝缘水平桌面上固定一个光滑绝缘的挡板ABCD、AB段为直线，BCD段是半径为R的圆弧，挡板处在场强为E的匀强电场中，电场方向与圆环直径MN平行。现使一带电荷量为＋q，质量为m的小球由静止从斜挡板内侧上某点释放，为使小球沿挡板内侧运动，从D点抛出，求：

(1)小球从释放点到N点沿电场强度方向的最小距离。
(2)在上问中小球经过N点时对挡板压力大小。

(14分)如图所示，固定在水平面上的斜面与水平面的连接处为一极小的光滑圆弧(物块经过Q点时不损失机械能)，斜面与地面是用同种材料制成的。斜面的最高点为P，P距离水平面的高度为h=5m。在P点先后由静止释放两个可视为质点的小物块A和B，A、B的质量均为m=1kg，A与斜面及水平面的动摩擦因数为μ1=0.5，B与斜面及水平面的动摩擦因数为μ2=0.3。A物块从P点由静止释放后沿斜面滑下，停在了水平面上的某处。

求：
(1)A物块停止运动的位置距离斜面的直角顶端O点的距离是多少?
(2)当A物块停止运动后准备再释放B物块时发现它们可能会发生碰撞，为了避免AB碰撞，此时对A另外施加了一个水平向右的外力F，把A物体推到了安全的位置，之后再释放B就避免了AB碰撞。求外力F至少要做多少功，可使AB不相撞?(g取10m/s2，此问结果保留三位有效数字)

如图所示，有一电子（电荷量为e，质量为m）经电压U0加速后，进入两块间距为d，电压为U的平行金属板间。若电子从两板正中间垂直电场方向射入，且正好能穿过电场，

求：（1）金属板AB的长度L； （2）电子穿出电场时的动能Ek。

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网