题目内容
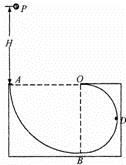
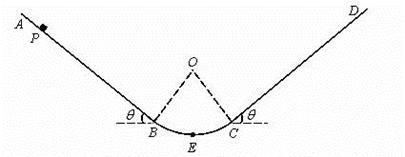
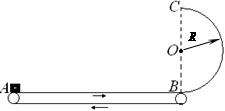
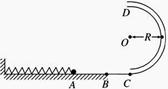
如图所示,光滑绝缘水平桌面上固定一个光滑绝缘的挡板ABCD、AB段为直线,BCD段是半径为R的圆弧,挡板处在场强为E的匀强电场中,电场方向与圆环直径MN平行。现使一带电荷量为+q,质量为m的小球由静止从斜挡板内侧上某点释放,为使小球沿挡板内侧运动,从D点抛出,求:
(1)小球从释放点到N点沿电场强度方向的最小距离。
(2)在上问中小球经过N点时对挡板压力大小。
(1) 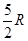 (2)6qE
(2)6qE
解析试题分析:(1)小球经过M点时恰好无压力,此时对应的s最小,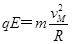 ①
①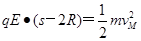 ②
②
由①②式解得s=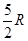 .
.
(2)过N点时,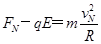 ③
③ ④
④
所以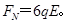
考点:圆周运动的向心力公式,动能定理,

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
探究能力是进行物理学研究的重要能力之一.物体因绕轴转动而具有的动能叫转动动能,转动动能的大小与物体转动的角速度有关.为了研究某一砂轮的转动动能Ek与角速度ω的关系,某同学采用了下述实验方法进行探索.如图所示,先让砂轮由动力带动匀速旋转,测得其角速度ω,然后让砂轮脱离动力,由于克服转轴间摩擦力做功,砂轮最后停下,测出砂轮脱离动力到停止转动的圈数n,通过分析实验数据得出结论.另外已测试砂轮转轴的直径为2 cm,转轴间的摩擦力为10 N/π.经实验测得的几组ω和n如下表所示:
| ω/rad·s-1 | 0.5 | 1 | 2 | 3 | 4 |
| n | 5.0 | 20 | 80 | 180 | 320 |
| Ek | | | | | |
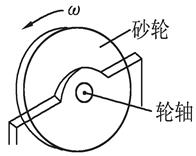
(1)计算出砂轮每次脱离动力的转动动能,并填入上表中.
(2)由上述数据推导出该砂轮的转动动能Ek与角速度ω的关系式为 .
(3)若测得脱离动力后砂轮的角速度为2.5 rad/s,则它转过45圈时的角速度为 rad/s 。
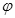 A>
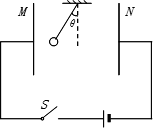
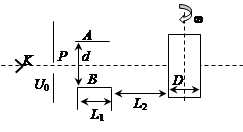
A>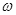 =4πrad/s的角速度匀速转动,确定电子在记录纸上的偏转位移随时间变化的关系式并定性画出1s钟内所记录的图形。(电子穿过AB的时间很短,可认为这段时间内板间电压不变)
=4πrad/s的角速度匀速转动,确定电子在记录纸上的偏转位移随时间变化的关系式并定性画出1s钟内所记录的图形。(电子穿过AB的时间很短,可认为这段时间内板间电压不变)
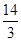 倍。取g=10m/s2。
倍。取g=10m/s2。