Question

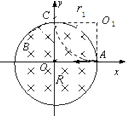
【题目】在以坐标原点O为圆心、半径为r的圆形区域内，存在磁感应强度大小为B、方向垂直于纸面向里的匀强磁场，如图所示．一个不计重力的带电粒子从磁场边界与x轴的交点A处以速度v沿﹣x方向射入磁场，它恰好从磁场边界与y轴的交点C处沿+y方向飞出．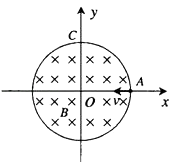

（1）请判断该粒子带何种电荷，并求出其比荷 ；
（2）若磁场的方向和所在空间范围不变，而磁感应强度的大小变为B′，该粒子仍从A处以相同的速度射入磁场，但飞出磁场时的速度方向相对于入射方向改变了60°角，求磁感应强度B′多大？此次粒子在磁场中运动所用时间t是多少？

Answer 1

【答案】
（1）解：由粒子的飞行轨迹，根据左手定则可知，该粒子带负电荷．

如图所示，

粒子由A点射入，由C点飞出，其速度方向改变了90°，

则粒子轨迹半径r1=r，

由qvB=m 得，粒子的荷质比为：

=

答：该粒子带负电荷；其比荷为

（2）解：粒子从D点飞出磁场速度方向改变了60°角，故AD弧所对圆心角为60°，

由几何知识可知，∠AO′O=30°，如图所示：

粒子做圆周运动的半径：R′=rcot30°= r，

又因为R′= ，

解得：B′= B．

粒子在磁场中飞行时间：

t= T= × =

答：磁感应强度B′为 B；粒子在磁场中飞行时间为

【解析】（1）粒子向上偏转，在A点受到的洛伦兹力方向向上，根据左手定则可判断粒子的电性．画出轨迹可知，粒子轨迹半径等于r，根据牛顿第二定律求解比荷；（2）根据粒子速度的偏向角等于轨迹的圆心角，求出轨迹的圆心角，来确定时间与周期的关系，求出时间．