题目内容
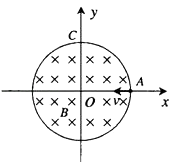
【题目】如图所示，一个质量为m、电荷量为e的粒子从容器A下方的小孔S，无初速度地飘入电势差为U的加速电场，然后垂直进入磁感应强度为B的匀强磁场中，最后打在照相底片M上．下列说法正确的是（ ）
A.粒子进入磁场时的速率 
B.粒子在磁场中运动的时间 
C.粒子在磁场中运动的轨道半径 
D.若容器A中的粒子有初速度，则粒子仍将打在照相底片上的同一位置
【答案】A,C
【解析】解：A、带电粒子在加速电场中运动，由动能定理有： 
得粒子进入磁场时的速率为： 
．故A正确．
B、C、粒子在磁场中做匀速圆周运动，由洛伦兹力提供向心力，则有： 
解得： 
= 
= 
．
所以周期T= 
，粒子在磁场中运动的时间t= 
= 
．故B错误、C正确．
D、若容器A中的粒子有初速度v0，则根据动能定理 
﹣ 
，得粒子进入磁场时的速率 
．
粒子在磁场中做匀速圆周运动，由洛伦兹力提供向心力，则有 
解得： 
= 
＞r．即若容器A中的粒子有初速度，则粒子打在照相底片上的不同的位置．故D错误．
故选：AC．
【考点精析】关于本题考查的带电微粒（计重力）在电场中的运动，需要了解带电颗粒:如液滴、油滴、尘埃、小球等，除有说明或明确的暗示以外，一般都不能忽略重力；由于带电粒子在匀强电场中所受电场力与重力都是恒力，因此可以用两种方法处理:①正交分解法;②等效“重力”法才能得出正确答案．
练习册系列答案
相关题目
