��Ŀ����
6�� ��ͼ��ʾ������Ǧ�=37��ֲ�б���ϣ�����һ�����߿�abcd�����У�ab�߳�L1=0.2m��bc�߳�L2=0.1m������m1=0.5kg������R=0.1�����߿���б��Ķ�Ħ��������=0.5���߿���ϸ��ͨ�������⻬��������һ���������������߿��ϸ����б��ƽ�У����������㹻�ߣ�����������m2=1.5kg��б����ef����gh�ߣ�ef��gh��ab�����д�ֱб�����ϵ���ǿ�ų����Ÿ�Ӧǿ��B=2.5T����ʼʱab����ų��±߽�ef�ľ���d1=0.34m���ų�����d2=1.3m���ֽ������ɾ�ֹ�ͷţ���ab�߸մӴų��ϱ�Եgh����ʱǡ��������ֱ���˶�����gȡ10m/s2��sin37��=0.6��cos37��=0.8����
��ͼ��ʾ������Ǧ�=37��ֲ�б���ϣ�����һ�����߿�abcd�����У�ab�߳�L1=0.2m��bc�߳�L2=0.1m������m1=0.5kg������R=0.1�����߿���б��Ķ�Ħ��������=0.5���߿���ϸ��ͨ�������⻬��������һ���������������߿��ϸ����б��ƽ�У����������㹻�ߣ�����������m2=1.5kg��б����ef����gh�ߣ�ef��gh��ab�����д�ֱб�����ϵ���ǿ�ų����Ÿ�Ӧǿ��B=2.5T����ʼʱab����ų��±߽�ef�ľ���d1=0.34m���ų�����d2=1.3m���ֽ������ɾ�ֹ�ͷţ���ab�߸մӴų��ϱ�Եgh����ʱǡ��������ֱ���˶�����gȡ10m/s2��sin37��=0.6��cos37��=0.8������1���߿��ab�߸մӴų��ϱ�Եgh����ʱ���������Ĺ��ʣ�
��2���߿�ո�ȫ������ų�ʱ�ٶȵĴ�С���߿��ų������в����Ľ����ȣ�
���� ��1����ƽ���������ab���˶���gh�ߴ����ٶȣ���P=Fv���ʣ�
��2���߿�ո�ȫ������ų�ʱ��ab�߸մӴų��ϱ�Եgh����ʱ���������غ�����ٶȣ��߿�ӳ�״̬����ȫ���ų������������غ㶨����⽹���ȣ�
��� �⣺��1����m2�У�T=m2g
��m1��T-��m1gcos��-m1gsin��-BIL1
E=BL1v
I=$\frac{E}{R}$
������ʽ�ɵ�v=4m/s
���ӵ���������P=Tv=m2gv=1.5��10��4=60W
��2���߿�ո�ȫ������ų�ʱ��ab�߸մӴų��ϱ�Եgh����ʱ���������غ�ã�
m2g��d2-L2��-����m1gcos��+m1gsin�ȣ���d2-L2��=$\frac{1}{2}$��m2+m1��v2$-\frac{1}{2}��{m}_{1}+{m}_{2}��{v}_{0}^{2}$
�������ݽⷽ�̵�v0=2m/s
�߿�ӳ�״̬����ȫ���ų����������غ㶨��֪��m2g��d1+d2+L2��-����m1gcos��+m1gsin�ȣ���d1+d2+L2��=$\frac{1}{2}$��m2+m1��v+Q
�������ݽⷽ�̵�Q=1.4J
�𣺣�1���߿��ab�߸մӴų��ϱ�Եgh����ʱ���������Ĺ���Ϊ60W��
��2���߿�ո�ȫ������ų�ʱ�ٶȵĴ�СΪ2m/s���߿��ų������в����Ľ�����Ϊ1.4J��
���� �����ǵ�Ÿ�Ӧ����ƽ�⡢�����غ㶨�ɵ��ۺϣ�ѡ����ʵĹ����ǹؼ�������������Ƚϴ���Ҫͬѧ�������������

| A�� | ǧ�ˣ�kg�� | B�� | �ף�m�� | C�� | ���϶ȣ��棩 | D�� | ţ�٣�N�� |
 ijͬѧ����ֱ���ҵĵ����¼ӹҹ��룬̽�������뵯���쳤���Ĺ�ϵ�����ɵĵ�����F��ʾ�����ɹ��Ϲ������쳤��x��ʾ�������Ǹ�ͬѧ��¼��ʵ�����ݣ�ʵ���е���ʼ��δ���������ȣ���g=10m/s2��
ijͬѧ����ֱ���ҵĵ����¼ӹҹ��룬̽�������뵯���쳤���Ĺ�ϵ�����ɵĵ�����F��ʾ�����ɹ��Ϲ������쳤��x��ʾ�������Ǹ�ͬѧ��¼��ʵ�����ݣ�ʵ���е���ʼ��δ���������ȣ���g=10m/s2����1������ʵ������������ϵ���������ɵĵ���F�뵯�ɵ��쳤��x�Ĺ�ϵͼ��
��2������ͼ��ɵõ��ɵľ���ϵ����25N/m��
| ����������m/g | 30 | 60 | 90 | 120 | 150 |
| �����쳤��x/cm | 1.2 | 2.4 | 3.6 | 4.8 | 6.4 |
 һ����Ϊm��С���ó�Ϊl������������O�㣬��һ��С����ˮƽ����F1�����£���ƽ��λ��P��ܻ������Ƶ�Q�㣬��ʱ������ֱ����н�Ϊ�ȣ���ͼ��ʾ���������������ˮƽ��������ΪW1���ڶ���С����ˮƽ����F2�����£���P���Ƶ�Q�㣬ˮƽ��������ΪW2���������ٶ�Ϊg���Ҧȣ�90�㣬������
һ����Ϊm��С���ó�Ϊl������������O�㣬��һ��С����ˮƽ����F1�����£���ƽ��λ��P��ܻ������Ƶ�Q�㣬��ʱ������ֱ����н�Ϊ�ȣ���ͼ��ʾ���������������ˮƽ��������ΪW1���ڶ���С����ˮƽ����F2�����£���P���Ƶ�Q�㣬ˮƽ��������ΪW2���������ٶ�Ϊg���Ҧȣ�90�㣬������| A�� | W1=F1lsin�ȣ�W2=F2lsin�� | B�� | W1=W2=mgl��1-cos�ȣ� | ||
| C�� | W1=mgl��1-cos�ȣ���W2=F2lsin | D�� | W1=F1lsin�ȣ�W2=mgl��1-cos�ȣ� |
| A�� | xΪ���ӣ���m1+m2-m3��C2 | B�� | xΪ���ӣ���m1+m2-m3��C2 | ||
| C�� | xΪ���ӣ���m1+m2-m3-m4��C2 | D�� | xΪ�����ӣ���m1+m2-m3-m4��C2 |
 һ����������ֻ�ڵ糡������������ֱ����A���˶���B�㣬�������ӵ�v-tͼ����ͼ��ʾ��������������ڵĵ糡�����ǣ�������
һ����������ֻ�ڵ糡������������ֱ����A���˶���B�㣬�������ӵ�v-tͼ����ͼ��ʾ��������������ڵĵ糡�����ǣ�������| A�� |  | B�� | 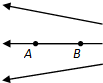 | C�� |  | D�� |  |
| A�� | ��ֱ���˶��У������λ�ƴ�С������·�� | |
| B�� | һ���������뷴����������������һ�����ڻ�С��0 | |
| C�� | ţ�ٸ�������б��ʵ�飬���������ά�������˶���ԭ�� | |
| D�� | �����յ�������$\frac{a^3}{T^2}$=KΪ�������˳����Ĵ�Сֻ���������������й� |
 ��ͼ��ʾ�������۰˺š��ɴ��롰�칬һ�š�Ŀ��������ڱ���ʱ��2011��11��3���賿ʵ�� �������ӣ��γ�����壬ʹ�й����˺����״οռ佻��Խ������óɹ�������֪������� ת����ΪT������뾶ΪR�����������������ٶ�Ϊg��������еĹ�������߶�Ϊh�������б���ʽ����ȷ���ǣ�������
��ͼ��ʾ�������۰˺š��ɴ��롰�칬һ�š�Ŀ��������ڱ���ʱ��2011��11��3���賿ʵ�� �������ӣ��γ�����壬ʹ�й����˺����״οռ佻��Խ������óɹ�������֪������� ת����ΪT������뾶ΪR�����������������ٶ�Ϊg��������еĹ�������߶�Ϊh�������б���ʽ����ȷ���ǣ�������| A�� | �����Χ�Ƶ�����Բ���˶������ٶȴ�v=$\frac{2�У�R+h��}{T}$ | |
| B�� | �����Χ�Ƶ�����Բ���˶��Ľ��ٶȴ�С��=$\sqrt{\frac{g}{R+h}}$ | |
| C�� | �����Χ�Ƶ�����Բ���˶�����������T��=$\sqrt{\frac{4{��}^{2}��R+h��^{3}}{g{R}^{2}}}$ | |
| D�� | ��������ڹ�������������ٶ�g��=$\frac{Rg}{R+h}$ |
