Question

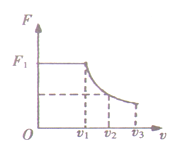
【题目】如图甲所示，一足够长、与水平面夹角θ＝53°的倾斜轨道与竖直面内的光滑圆轨道相接，圆轨道的半径为R，其最低点为A，最高点为B。可视为质点的物块与斜轨间有摩擦，物块从斜轨上某处由静止释放，到达B点时与轨道间压力的大小F与释放的位置距最低点的高度h的关系图象如图乙所示。忽略轨道相接处距最低点的高度，且不计物块通过轨道相接处时的能量损失，取重力加速度g＝10 m/s2，sin53°＝，cos53°＝，求：

(1)物块与斜轨间的动摩擦因数μ；

(2)物块的质量m。

Answer 1

【答案】(1) (2)0.2 kg

【解析】

（1）由题图乙可知，当h1＝5R时，物块到达B点时与轨道间压力的大小为0，设此时物块在B点的速度大小为v1，则

mg＝

对物块从释放至到达B点的过程，由动能定理有

mg(h1－2R)－μmgcosθ ＝mv

解得

μ＝

（2）设物块从距最低点高为h处释放后到达B点时速度的大小为v，则

F＋mg＝

物块从释放至到达B点的过程中，由动能定理有

mg(h－2R)－μmgcosθ＝mv2

解得

F＝－5mg，

此解析式为乙图中的图线的表达式，则F-h图线的斜率k＝

由题图乙可知k＝，

解得

m＝0.2 kg