题目内容
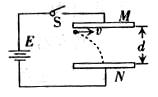
一个带电粒子以初速度 与水平方向成q 角(sinq =0.6)斜向上射入某匀强电场区域,粒子进入电场区域后沿直线运动.已知:粒子的质量为m=7.5×
与水平方向成q 角(sinq =0.6)斜向上射入某匀强电场区域,粒子进入电场区域后沿直线运动.已知:粒子的质量为m=7.5× kg,带电量q=4×
kg,带电量q=4× C,取
C,取 ,带电粒子所受的重力不能忽略.
,带电粒子所受的重力不能忽略.
(1)要使带电粒子进入电场后沿直线运动,求:该电场电场强度的最小值及方向.
(2)当电场强度为最小值时,通过计算说明该粒子进入这个电场区域后运动的性质.
 与水平方向成q 角(sinq =0.6)斜向上射入某匀强电场区域,粒子进入电场区域后沿直线运动.已知:粒子的质量为m=7.5×
与水平方向成q 角(sinq =0.6)斜向上射入某匀强电场区域,粒子进入电场区域后沿直线运动.已知:粒子的质量为m=7.5× kg,带电量q=4×
kg,带电量q=4× C,取
C,取 ,带电粒子所受的重力不能忽略.
,带电粒子所受的重力不能忽略.(1)要使带电粒子进入电场后沿直线运动,求:该电场电场强度的最小值及方向.
(2)当电场强度为最小值时,通过计算说明该粒子进入这个电场区域后运动的性质.
(1)1.5× N/C 方向:垂直于
N/C 方向:垂直于 斜向上.(2)
斜向上.(2)
 N/C 方向:垂直于
N/C 方向:垂直于 斜向上.(2)
斜向上.(2)
(1)带电粒子受重力和电场力如图所示. (2分)
要使带电粒子沿直线运动,其初速度方向必与合外力方向共线,必须使粒子在垂直于运动直线方向上所受合力为零.要使电场强度最小,匀强电场方向应垂直于运动直线(或 )向上,即:使电场力与重力在垂直于运动直线方向上的分力互相平衡. (2分)
)向上,即:使电场力与重力在垂直于运动直线方向上的分力互相平衡. (2分)
设E为满足条件的电场强度的最小值并满足方程:
 (2分)
(2分)
得: (2分)
(2分)
代入数据:E=1.5× N/C (2分)
N/C (2分)
方向:垂直于 斜向上. (2分)
斜向上. (2分)
(2)由于粒子所受重力、电场力均为恒力,所以粒子的加速度恒定.粒子所受的合外力方向与 方向相反,所以粒子做匀减速运动. (3分)
方向相反,所以粒子做匀减速运动. (3分)
由:mgsinq =ma解得: (3分)
(3分)

要使带电粒子沿直线运动,其初速度方向必与合外力方向共线,必须使粒子在垂直于运动直线方向上所受合力为零.要使电场强度最小,匀强电场方向应垂直于运动直线(或
 )向上,即:使电场力与重力在垂直于运动直线方向上的分力互相平衡. (2分)
)向上,即:使电场力与重力在垂直于运动直线方向上的分力互相平衡. (2分)设E为满足条件的电场强度的最小值并满足方程:
 (2分)
(2分)得:
 (2分)
(2分)代入数据:E=1.5×
 N/C (2分)
N/C (2分)方向:垂直于
 斜向上. (2分)
斜向上. (2分)(2)由于粒子所受重力、电场力均为恒力,所以粒子的加速度恒定.粒子所受的合外力方向与
 方向相反,所以粒子做匀减速运动. (3分)
方向相反,所以粒子做匀减速运动. (3分)由:mgsinq =ma解得:
 (3分)
(3分)

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目