题目内容
6. 如图所示为一小球做平抛运动的闪光照相照片的一部分,图中背景方格的边长均为1.25cm,如果取g=10m/s2,那么:
如图所示为一小球做平抛运动的闪光照相照片的一部分,图中背景方格的边长均为1.25cm,如果取g=10m/s2,那么:(1)照相机的闪光频率是20Hz;
(2)小球运动中水平分速度的大小是1m/s;
(3)小球经过A点时的速度大小是$\sqrt{1.25}$m/s.(结果可用根式表示)
分析 (1)根据竖直方向上连续相等时间内的位移之差是一恒量求出相等的时间间隔,从而得出闪光的频率.
(2)根据水平位移和时间间隔求出小球运动过程中的水平分速度大小.
(3)根据某段时间内的平均速度等于中间时刻的瞬时速度求出B点的竖直分速度,结合速度时间公式求出A点的竖直分速度,根据平行四边形定则求出A点的速度.
解答 解:(1)在竖直方向上,根据△y=2L=gT2得:T=$\sqrt{\frac{2L}{g}}=\sqrt{\frac{2×1.25×1{0}^{-2}}{10}}s=0.05s$,
则闪光的频率为:f=$\frac{1}{T}=\frac{1}{0.05}Hz=20Hz$.
(2)小球运动的水平分速度为:${v}_{x}=\frac{4L}{T}=\frac{4×1.25×1{0}^{-2}}{0.05}m/s=1m/s$.
(3)B点竖直分速度为:${v}_{yB}=\frac{8L}{2T}=\frac{8×1.25×1{0}^{-2}}{0.1}m/s=1m/s$,
则A点竖直分速度为:vyA=vyB-gT=1-10×0.05m/s=0.5m/s.
根据平行四边形定则知,A点的速度为:${v}_{A}=\sqrt{{{v}_{yA}}^{2}+{{v}_{x}}^{2}}=\sqrt{0.25+1}$m/s=$\sqrt{1.25}$m/s.
故答案为:20,(2)1,(3)$\sqrt{1.25}$.
点评 解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,结合运动学公式和推论灵活求解,难度中等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.气象卫星向地面发送的卫星云图,是由卫星上的红外线感应器接收云层发出的红外线而形成的图象,云图上的黑白程度由云层的温度高低决定,这是利用红外线的( )
| A. | 衍射能力强 | B. | 穿透性 | C. | 热效应 | D. | 化学效应 |
15.某个物体的位移与时间的函数关系为x=3t+5t2(x以m为单位,t以s为单位),下列说法中正确的是( )
| A. | 这个物体的初速度是3m/s | |
| B. | 这个物体的加速度大小是5m/s2 | |
| C. | 这个物体的初速度是1.5m/s | |
| D. | 这个物体加速度方向一定与初速度方向一致 |
16.某电视台的娱乐节目中有-“搬运”的项目,比谁搬得快,某次节目中,要求将并排放在水平地面上的10块质量均为5kg、边长均为0.3m的正方体(质量分布均匀)变为竖直叠放,若此比赛中冠军获得者用时为15s,重力加速度g=10m/s2,则该冠军做功的最小值及最小的平均功率分别为( )
| A. | 600J 40W | B. | 1500J 40W | C. | 675J 15W | D. | 675J 45W |
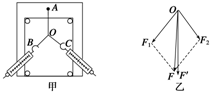 某同学做“探究力的平行四边形定则”的实验情况如图甲所示,A为固定橡皮条的图钉,O为橡皮条与细绳的结点,OB和OC为细绳.图乙是在白纸上根据实验结果画出的图.
某同学做“探究力的平行四边形定则”的实验情况如图甲所示,A为固定橡皮条的图钉,O为橡皮条与细绳的结点,OB和OC为细绳.图乙是在白纸上根据实验结果画出的图. 一个质量为m,带电量为q的带正电粒子(不计重力),以沿x轴正方向的初速运动,从图中y轴上离原点$\frac{R}{2}$处开始进入一个圆心在(R,0),方向垂直于纸面向外边界为圆形的匀强磁场中,磁感应强度大小为B,磁场半径为R,粒子在磁场中运动的轨道半径比磁场半径R大.若粒子经过了磁场中的最大位移,求粒子的速度大小及运动时间?
一个质量为m,带电量为q的带正电粒子(不计重力),以沿x轴正方向的初速运动,从图中y轴上离原点$\frac{R}{2}$处开始进入一个圆心在(R,0),方向垂直于纸面向外边界为圆形的匀强磁场中,磁感应强度大小为B,磁场半径为R,粒子在磁场中运动的轨道半径比磁场半径R大.若粒子经过了磁场中的最大位移,求粒子的速度大小及运动时间?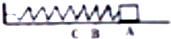 如图所示,轻质弹簧左端固定,右端与质量为m的物块连接,物块可在光滑水平面上运动,现将物块拉至水平面上的A点并无初速度释放,当物块经过B点时速度为v,弹簧为原长状态,当物块经过C点时速度为$\frac{v}{2}$,求:
如图所示,轻质弹簧左端固定,右端与质量为m的物块连接,物块可在光滑水平面上运动,现将物块拉至水平面上的A点并无初速度释放,当物块经过B点时速度为v,弹簧为原长状态,当物块经过C点时速度为$\frac{v}{2}$,求: 为了减少汽车刹车失灵造成的危害,如图所示为高速路上在下坡路段设置的可视为斜面的紧急避险车道,一辆货车在倾角θ=30°的连续长直下坡高速路上,以v0=7m/s的速度在刹车状态下匀速行驶(在此过程及后面过程中,可认为发动机不提供牵引力),突然汽车刹车失灵,开始加速运动,此时汽车所受到的摩擦和空气阻力共为车重的0.45,在加速前进了x0=96m后,货车冲上了平滑连接的倾角α=53°避险车道,己知货车在该避险车道上所受到的摩擦和空气阻力共为车重的0.45.货车的各个运动过程均可视为直线运动.sin53°=0.8,g=10m/s2.求:
为了减少汽车刹车失灵造成的危害,如图所示为高速路上在下坡路段设置的可视为斜面的紧急避险车道,一辆货车在倾角θ=30°的连续长直下坡高速路上,以v0=7m/s的速度在刹车状态下匀速行驶(在此过程及后面过程中,可认为发动机不提供牵引力),突然汽车刹车失灵,开始加速运动,此时汽车所受到的摩擦和空气阻力共为车重的0.45,在加速前进了x0=96m后,货车冲上了平滑连接的倾角α=53°避险车道,己知货车在该避险车道上所受到的摩擦和空气阻力共为车重的0.45.货车的各个运动过程均可视为直线运动.sin53°=0.8,g=10m/s2.求: