题目内容
15.自由落体在最后1s内通过的路程与最后1s的前1s内所通过路程的大小之比为$\frac{3}{2}$,求自由落体的初始位置离地面的高度.(g=10m/s2)分析 对在最后1s内通过的路程与最后1s的前1s内所通过路程列自由落体的位移与时间关系,联立可求得时间及位移.
解答 解:在最后1s内通过的路程:${h}_{1}=\frac{1}{2}g{t}^{2}-\frac{1}{2}g(t-1)^{2}$
${h}_{2}=\frac{1}{2}g({t-1)}^{2}-\frac{1}{2}g{(t-2)}^{2}$
又:$\frac{{h}_{1}}{{h}_{2}}=\frac{3}{2}$
联立得:t=3.5s
自由落体的初始位置离地面的高度:$h=\frac{1}{2}{gt}^{2}=\frac{1}{2}×10×3.{5}^{2}=61.25$m
答:自由落体的初始位置离地面的高度是61.25m.
点评 本题考查自由落体运动的规律,要注意我们通常从下落点开始列式求解,这样可以简化计算过程.

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案
相关题目
6.下列关于力的叙述正确的有( )
| A. | 力是物体对物体的作用,总是成对出现的 | |
| B. | 只有相互接触的物体,才有力的作用 | |
| C. | 物体相互作用一定直接接触 | |
| D. | 力不能离开物体而存在 |
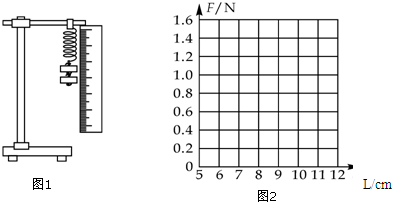
10.利用如图1所示装置做探索弹力和弹簧伸长的关系的实验.所用的钩码每只的质量30g.实验中,先测出不挂钩码时弹簧的自然长度,再将5个钩码逐个加挂在弹簧下端,稳定后测出相应的弹簧总长度,将数据填在表中.(弹力始终未超过弹性限度,取g=9.8m/s2)
(1)如表记录弹簧总长,数据中有一个不合规范,应记作8.20cm.
(2)根据实验数据,将第2组弹力大小计算出来并填入表内相应的空格内(保留3位有效数字).
(3)在坐标纸中(如图2)作出弹簧弹力大小F跟弹簧总长度L之间的函数关系的图线.
(4)由图线求得该弹簧的劲度k=26.6N/m.

(1)如表记录弹簧总长,数据中有一个不合规范,应记作8.20cm.
(2)根据实验数据,将第2组弹力大小计算出来并填入表内相应的空格内(保留3位有效数字).
| 记录数据组 | 1 | 2 | 3 | 4 | 5 | 6 |
| 钩码总质量(g) | 0 | 30 | 60 | 90 | 120 | 150 |
| 弹簧总长(cm) | 6.00 | 7.11 | 8.2 | 9.31 | 10.40 | 11.52 |
| 弹力大小(N) | 0 | 0.588 | 0.882 | 1.176 | 1.47 |
(4)由图线求得该弹簧的劲度k=26.6N/m.
5.一支长150m的队伍匀速前进,通信员从队尾前进300m后赶到队首,传达命令后立即返回,当通信员回到队尾时,队伍已前进了200m,则在此全过程中,通信员的位移和路程分别是( )
| A. | 300m 500m | B. | 300m 400m | C. | 200m 500m | D. | 200m 400m |
 如图所示,两根金属导轨平行放置在倾角为θ=30°的斜面上,导轨下端接有定值电阻R=10Ω,导轨自身电阻忽略不计.导轨置于垂直于斜面向上的匀强磁场中,磁感应强度B=0.5T.将一根质量为m=0.1kg、电阻可不计的金属棒ab在导轨上方某处由静止释放,金属棒沿导轨下滑(金属棒ab与导轨间的摩擦不计).设导轨足够长,导轨宽度L=2m,金属棒ab下滑过程中始终与导轨接触良好,当金属棒沿导轨下滑的高度h=3m时,速度恰好达到最大值.此过程中(g=10m/s2),求:
如图所示,两根金属导轨平行放置在倾角为θ=30°的斜面上,导轨下端接有定值电阻R=10Ω,导轨自身电阻忽略不计.导轨置于垂直于斜面向上的匀强磁场中,磁感应强度B=0.5T.将一根质量为m=0.1kg、电阻可不计的金属棒ab在导轨上方某处由静止释放,金属棒沿导轨下滑(金属棒ab与导轨间的摩擦不计).设导轨足够长,导轨宽度L=2m,金属棒ab下滑过程中始终与导轨接触良好,当金属棒沿导轨下滑的高度h=3m时,速度恰好达到最大值.此过程中(g=10m/s2),求: