题目内容
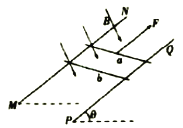
【题目】如图所示，两端开口的U形管粗细均匀，左右两管竖直，底部的直管水平，水银柱的长度如图中标注所示，水平管内两端空气柱a、b的长度分别为10cm、5cm。在左管内缓慢注入一定量的水银，稳定后右管的水银面比原来高10cm。已知大气压强P0＝76cmHg，管内外的温度相同且始终不变。求向左管注入的水银柱长度。
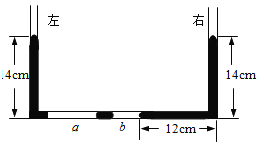
【答案】21.5cm
【解析】初状态a、b两部分空气柱的压强：P1＝90cmHg
因右管水银面升高的高度10cm＜12cm，故b空气柱仍在水平管内。末状态a、b两部分空气柱的压强：P2＝100cmHg
设末状态a、b两部分空气柱的长度分别为La2、Lb2
对a、b两部分空气柱分别根据玻意耳定律可得：
P1·La1S＝P2·La2S ①
P1·Lb1S＝P2·Lb2S ②
代入数据，联立①②式解得：La2＝9cm Lb2＝4.5cm
设左管注入的水银柱长度为L，则：L=2h+（La1+ Lb1）－（La2+ Lb2）=21.5cm
另解：初状态a、b两部分空气柱的压强：P1＝90cmHg
因右管水银面升高的高度10cm＜12cm，故b空气柱仍在水平管内。末状态a、b两部分空气柱的压强：P2＝100cmHg（
A、b两部分空气柱的初、末温度及初、末压强均相等，将它们看成一个整体，则初状态的长度为L1=15cm，末状态的长度设为L2=xcm，则由玻意耳定律可得：
P1·L1S＝P2·L2S ①
由①式解得：L2＝13.5cm ②
所以左侧注入水银柱的长度为L＝10+10+（15－L2）＝21.5cm③
练习册系列答案
全优点练单元计划系列答案
相关题目
