题目内容
【题目】一个半圆柱形玻璃砖,其横截面是半径为R的半圆,AB为半圆的直径,O为圆心,如图所示,玻璃的折射率n=![]() .
.
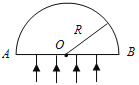
(i)一束平行光垂直射向玻璃砖的下表面,若光线到达上表面后,都能从该表面射出,则入射光束在AB上的最大宽度为多少?
(ii)一细束光线在O点左侧与O相距![]() R处垂直于AB从下方入射,求此光线从玻璃砖射出点的位置.
R处垂直于AB从下方入射,求此光线从玻璃砖射出点的位置.
【答案】(i)一束平行光垂直射向玻璃砖的下表面,若光线到达上表面后,都能从该表面射出,则入射光束在AB上的最大宽度为![]() R;
R;
(ii)一细束光线在O点左侧与O相距![]() R处垂直于AB从下方入射,此光线从玻璃砖射出点的位置在O点左侧或者右侧
R处垂直于AB从下方入射,此光线从玻璃砖射出点的位置在O点左侧或者右侧![]() R处.
R处.
【解析】解:(i)根据全反射定律:sinC=![]() ,
,
得:C=45°,
即临界角为45°,如下图:

由几何知识得:d=![]() ,
,
则入射光束在AB上的最大宽度为2d=![]() R;
R;
(ii)设光线在距离O点![]() R的C点射入后,在上表面的入射角为α,由几何关系和已知条件得:α=60°>C
R的C点射入后,在上表面的入射角为α,由几何关系和已知条件得:α=60°>C
光线在玻璃砖内会发生三次全反射,最有由G点射出,如图:
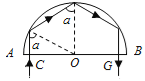
由反射定律和几何关系得:
OG=OC=![]() R,
R,
射到G点的光有一部分被反射,沿原路返回到达C点射出.
答:(i)一束平行光垂直射向玻璃砖的下表面,若光线到达上表面后,都能从该表面射出,则入射光束在AB上的最大宽度为![]() R;
R;
(ii)一细束光线在O点左侧与O相距![]() R处垂直于AB从下方入射,此光线从玻璃砖射出点的位置在O点左侧或者右侧
R处垂直于AB从下方入射,此光线从玻璃砖射出点的位置在O点左侧或者右侧![]() R处.
R处.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目