Question

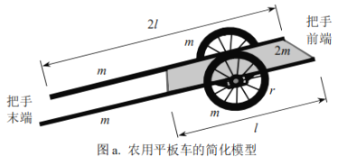
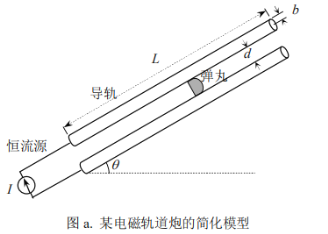
【题目】某电磁轨道炮的简化模型如图a所示，两圆柱形固定导轨相互平行，其对称轴所在平面与水平面的夹角为θ，两导轨的长均为L、半径均为b、每单位长度的电阻均为，两导轨之间的最近距离为d(d很小).一弹丸质量为m(m较小)的金属弹丸(可视为薄片)置于两导轨之间，弹丸直径为d、电阻为R，与导轨保持良好接触.两导轨下端横截面共面，下端(通过两根与相应导轨同轴的、较长的硬导线)与一电流为I的理想恒流源(恒流源内部的能量损耗可不计)相连，不考虑空气阻力和摩擦阻力，重力加速度大小图a.某电磁轨道炮的简化模型为g，真空磁导率为μ0.考虑一弹丸自导轨下端从静止开始被磁场加速直至射出的过程.

(1)求弹丸在加速过程中所受到的磁场作用力；

(2)求弹丸的出射速度；

(3)求在弹丸加速过程中任意时刻、以及弹丸出射时刻理想恒流源两端的电压；

(4)求在弹丸的整个加速过程中理想恒流源所做的功:

(5)在θ=0°的条件下，若导轨和弹丸的电阻均可忽略，求弹丸出射时的动能与理想恒流源所做的功之比.

Answer 1

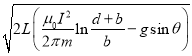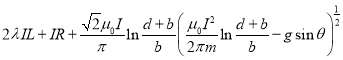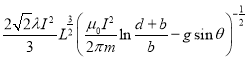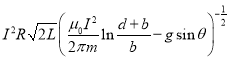
【答案】（1） 方向平行于导轨轴线斜向上 （2）方向平行于导轨轴线斜向上 （3）（4），（5）50%

【解析】

(1)由于弹丸直径d很小，每根载流导轨均可视为半无限长载流直导线，弹丸上离某导轨轴线距离为r′处的磁场的磁感应强度大小为

(1)

方向垂直于两导轨对称轴所在平面斜向下。弹丸长为的一段所受到的磁场作用力(安培力)为

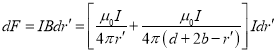(2)

方向平行于导轨轴线斜向上.弹丸所受到的安培力大小为

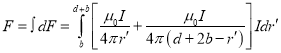
(3)

方向平行于导轨轴线斜向上，

(2)设弹丸的加速度大小为.由牛顿第二定律有

(4)

由(3)(4)式得，弹丸的加速度大小为

(5)

方向平行于导轨轴线斜向上.

弹丸作匀加速直线运动，弹丸的出射速度满足

(6)

由(5)(6)式得

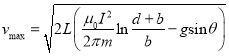(7)

方向平行于导轨轴线斜向上.

(3)两导轨之间离某导轨轴线距离为r处(不一定是弹丸上一点)的磁场为

(8)

通过两导轨各自从下端开始长为l的一段以及弹丸长为dr的一-段组成平面回路的磁通量为

(9)

通过两导轨各自从下端开始长为l的一段以及弹丸组成平面回路的磁通量为

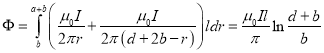(10)

根据法拉第电磁感应定律，回路中的感应电动势为

(11)

式中是弹丸沿导轨的运动速度.由全电路欧姆定律得

(12)

式中U为恒流源两端的电压。弹丸做匀加速直线运动，在通电后任意时刻t有

(13)

(14)

由(11)(12)(13)(14)式得，在时刻t恒流源两端的电压为

即

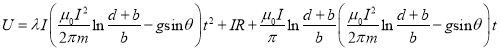(14)

由(7)(13)式得，弹丸的加速度时间为

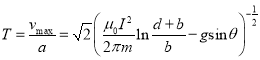(16)

由(15)(16)式得，弹丸出射时电源两端的电压为

(17)

(4)在弹丸的整个加速过程中，恒流源所做的功为

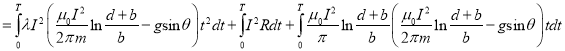(18)

下面依次计算(18)式右端的第一项、第二项，和第三项:

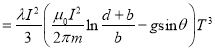
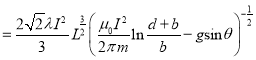(19)

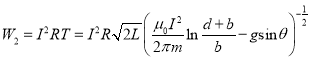
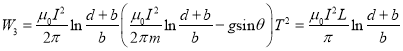
(5)弹丸出射时的动能为:

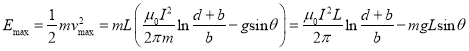(20)

在的条件下，弹丸出射时的动能为

(21)

若导轨和弹丸的电阻可忽略，恒流源所做的功为

(22)

弹丸出射时的动能与恒流源所做的功之比

=50% (23)