��Ŀ����
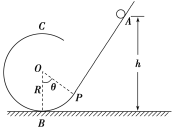
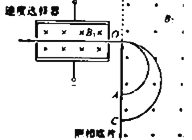
����Ŀ����ͼ����ʾ��ˮƽ���AB����ֱ���ڰ뾶ΪR=0.1m�Ĺ⻬����״Բ���O�����Ϊ��=37��б��BD�������ƽ�����ӡ�һ����ΪM=0.1kg�����˶�����Ϊ��ͷ����С�����С����װ�м��ٶ���ʾ������ͼ������Ŵ�ͼ�����������˷ֱ������Ӻ�С����������ֹʱ���ɴ���ԭ��λ�ã�ָ��λ����0���̶ȴ�����ʹС����������������ˮƽ���AB�Լ��ٶ�a=2m/s2�Ӿ�ֹ��ʼ������B�㣬֮��ȥ����С����Բ��������˶���������б��BD����֪С���ڳ���б��BDʱָ���뿪��0���̶�2mm�����������ɾ���ϵ��Ϊk=10N/m����������Ϊm=0.01kg���복����Ħ������
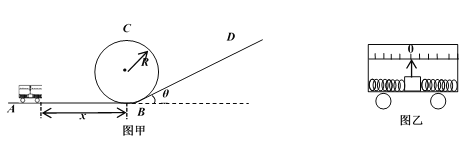
(1)С������б��BDʱ����ʾ��ָ��λ����0���̶������ҷ���С����б��Ķ�Ħ��������Ϊ���٣�
(2)ҪʹС���ܹ�����AB���ϣ�������BD�����˶������ʱ��tmin��
(3)ҪʹС��������������С����ʼ�˶�ʱ��������AB�������õľ���x�����������
���𰸡�(1)�ҷ� �ɵ�![]() (2)
(2) (3)
(3) ![]() ��
��![]()
��������
(1)��С��Ϊ�о������֪��С����������Ħ��������ţ�ٵڶ�����![]() ��֪��С���ļ��ٶȴ���
��֪��С���ļ��ٶȴ���![]() ��
��
������Ϊ�о�����ֻ�е������ҷ����ɴ���ѹ��״̬�����ɴ�������״̬ʱ�����ӵļ��ٶȴ���![]() ��������ʾ��ָ��λ����0���̶ȵ��ҷ���
��������ʾ��ָ��λ����0���̶ȵ��ҷ���
������Ϊ�о�����![]()
![]()
��С��Ϊ�о�����![]()
�ɵ�![]() ��
��
(2)ǡ�ܷ���AB�棬��ʱ![]()
��ʱ��B���ٶ�Ϊ![]()
��б���»��ļ��ٶ�![]()
�»�![]() ��
�� ![]()
���![]() ��
��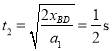

(3)���һ������б����ܻص�AB�棬֪![]()
![]() ��
��![]()
![]() ,
, ![]()
���� ![]()
�����������б���ص���Բ�ĵȸߴ���
�ܹ���ߵ�C ![]() ,
,![]()
ǡ�ûص���Բ�ĵȸߴ���![]() ��
��![]() ��
�� ![]()
���һ�ε���B��ʱ ![]()
![]()
�� ![]() ��
�� ![]()
���� ![]()

 ��У����ϵ�д�
��У����ϵ�д�