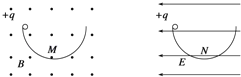Question

【题目】匀强电场中a、b、c三点，在以它们为顶点的三角形中，∠a＝30°、∠c＝90°.电场方向与三角形所在平面平行．已知a、b和c点的电势分别为(2－)V、(2＋)V和2V．该三角形的外接圆上最低电势为________；最高电势为______________．

Answer 1

【答案】0，4

【解析】试题分析：作出三角形的外接圆，其圆心O在ab的中点，该点电势为2V，OC为等势线，作出OC的垂线MN为电场线，根据U=Ed，顺着电场线MN，找出离O点最远的点，电势最低；逆着电场线，离O点最远点电势最高．

解：如图所示，取ab的中点O，即为三角形的外接圆的圆心，则：

O点的电势为：φO==V=2V

故Oc为等势线，其垂线MN为电场线，方向为：M→N．

所以外接圆上电势最低点为N点，最高点为M点．

设外接半径为R，则Op间的电势差等于Oa间的电势差，即：

UOP=UOa=2V﹣（2﹣）V=V，

又 UON=ER，UOP=ERcos30°，

则：UON：UOP=2：，

故有：UON=2V，N点电势为零，为最低电势点，

同理M点电势为4V，为最高电势点．

故答案为：0，4．