题目内容
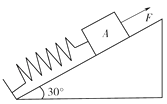
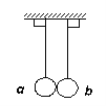
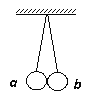
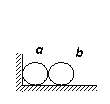
【题目】如图所示，两个半径相同的半圆形轨道分别竖直放置在匀强电场和匀强磁场中．轨道两端在同一高度上，轨道是光滑的，两个相同的带正电小球同时从两轨道左端最高点由静止释放．M、N为轨道的最低点，则下列说法正确的是（ ）
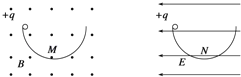
A．两小球到达轨道最低点的速度vM＜vN
B．两小球第一次到达轨道最低点时对轨道的压力FM＜FN
C．小球第一次到达M点的时间大于小球第一次到达N点的时间
D．在磁场中小球能到达轨道的另一端，在电场中小球不能到达轨道的另一端
【答案】D
【解析】
试题分析：两个轨道的半径相同，根据圆周运动的向心力的公式可以分析小球通过最低点是对轨道的压力，小球在磁场中运动，磁场力对小球不做功，整个过程中小球的机械能守恒，小球在电场中受到的电场力对小球做负功，到达最低点时的速度的大小较小．
解：AC、在磁场中运动时，只有重力做正功，在电场中运动时，重力做正功、电场力做负功，由动能定理可知：
mv
=mgH
mv
=mgH﹣qEd
解得，vM＞vN，由于小球在磁场中运动，磁场力对小球不做功，整个过程中小球的机械能守恒；而小球在电场中运动受到的电场力对小球做负功，到达最低点时的速度的大小较小，所以在电场中运动的时间也长，故AC错误；
B、最低点M时，支持力与重力和洛伦兹力（方向竖直向下）的合力提供向心力，最低点N时，支持力与重力的合力提供向心力，因为vM＞vN，可知：FM＞FN，故B错误；
D、由于小球在磁场中运动，磁场力对小球不做功，整个过程中小球的机械能守恒，所以小球可以到达轨道的另一端，而电场力做小球做负功，所以小球在达到轨道另一端之前速度就减为零了，故不能到达最右端，故D正确；
故选：D．
天天向上一本好卷系列答案
小学生10分钟应用题系列答案【题目】某同学在用小车做“测定匀变速直线运动的加速度”实验时，从打出的若干纸带中选出了如下图所示的一条，每相邻两点间还有四个计时点没有画出，上部的字母为相邻两计数点间的距离，其中x1=2.92cm，x2=5.10cm，x3=7.14cm，x4=9.02cm，x5=10.90cm，x6=12.98cm。打点计时器的电源频率为50Hz。
（1）根据纸带数据计算各计数点的瞬时速度写进表格，请填写下表中未计算的瞬时速度。（计算结果保留2位小数）
计数点 | A | B | C | D | E |
瞬时速度m/s | 0.40 | _____ | 0.81 | 1.00 | 1.19 |
（2）请以O点为计时起点在右图中画出小车运动的v-t图象，并根据v-t图象求出匀变速直线运动的加速度a=___m/s2 （计算结果保留3位有效数字）。
（3）该同学再利用所测距离借助公式计算加速度，请用题中所给符号写出最合理的计算加速度的表达式a=________（相邻计数点的时间间隔用T表示）。
